2015-05-20
383
При большом количестве узлов интерполяции сильно возрастает степень интерполяционных многочленов, что делает их неудобными для вычислений. Высокой степени многочлена можно избежать, разбив отрезок интерполяции на несколько частей с построением на каждой части самостоятельного интерполяционного многочлена.
1. Кусочно-линейная интерполяция
Простейшим, часто используемым видом локальной интерполяции, является кусочно-линейная интерполяция. Она состоит в том, что заданные точки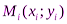 
(
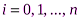) соединяются прямолинейными отрезками, а функция 
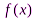приближается к ломаной с вершинами в данных точках.
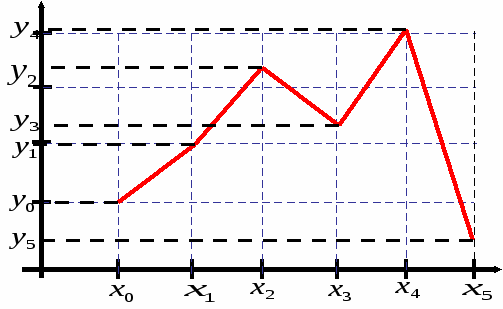
Для каждого из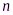 
интервалов 
, (
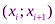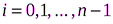) в качестве уравнения интерполяционного многочлена используется уравнение прямой, проходящей через две точки 
, 
:
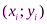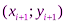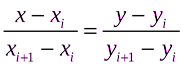(1)
Следовательно, при использовании кусочно-линейной интерполяции сначала необходимо определить интервал, в который попадает значение аргумента 
, затем подставить значение 
в формулу (1) для найденного интервала и найти приближенное значение функции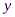 
. Можно показать, что интерполирование по формуле (1) тождественно интерполированию с помощью интерполяционного многочлена Лагранжа первой степени (
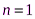) для точек 
, 
:
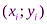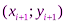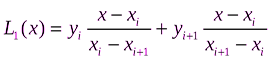(2)
Формулы (1) и (2) эквивалентны.
