Дать постановку задачи интерполяции

Вопросы на 2 балла.

Дать определение одношагового итерационного метода.

Определение 1. 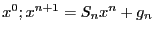-- общий вид одношагового нестационарного итерационного метода. Если 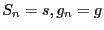, то метод называется стационарным. Можно записать метод в канонической форме

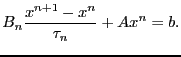
Тогда метод называется явным, если 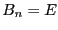, иначе неявный. Для перехода к общему виду в случае явного метода достаточно положить

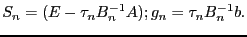
Дать определения к-шагового итерационного метода.

Дать определение итерационного метода, сходящегося со скоростью геометрической прогрессии.

Дать определение порядка сходимости итерационного метода.

Дать постановку задачи интерполяции.

Простейшая задача интерполяции заключается в следующем. На отрезке [ a, b ] заданы n + 1 точки x_i = х ₀, х ₁ ,..., х_n, которые называются узлами интерполяции, и значения некоторой функции f (x) в этих точках

f (x 0) = y 0, f (x 1) = y 1 ,..., f (xn) = yn.

(1)

Требуется построить функцию F (х) (интерполяционная функция), принадлежащую известному классу и принимающую в узлах интерполяции те же значения, что и f (x), т. е. такую, что

F(x 0) = y 0, F(x 1) = y 1 ,..., F(xn) = yn.

(2)

Геометрически это означает, что нужно найти кривую y = F (х) некоторого определенного типа, проходящую через заданную систему точек M(x_i, y_i) (i = 0, 1 ,..., n) (Рисунок 1).

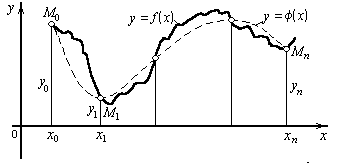
Рисунок 1

В такой общей постановке задача может иметь бесконечное множество решений или совсем не иметь решений.

Однако эта задача становится однозначной, если вместо произвольной функции F (х) искать полином j (х) (интерполяционный полином) степени не выше n, удовлетворяющий условиям (2), т. е. такой, что

j (x 0) = y 0, j (x 1) = y 1 ,..., j(xn) = yn.	(3)

ну или: требуется восстановить функцию f(x) для всех значений x 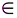[a, b] если известны её значения в некотором конечном числе точек этого отрезка.