Продолжительность 2 часа
Цель: научиться выполнению алгоритма Дейкстры.
Рекомендации студентам по подготовке к занятию: [3] Глава 3. §4 Кратчайшие пути
Теоретические сведения. Припишем всем ребрам графа веса – положительные числа. Кратчайший путь от вершины 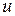 до вершины
до вершины 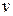 – это маршрут от
– это маршрут от 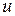 до
до 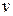 с минимальной суммой весов ребер маршрута.
с минимальной суммой весов ребер маршрута.
Задача о кратчайшем пути на графе. Надо найти все кратчайшие пути от данной вершины до всех остальных вершин.
Определение алгоритма Дейкстры. Каждой вершине 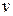 ставим метку – минимальное известное расстояние от данной вершины
ставим метку – минимальное известное расстояние от данной вершины 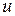 .
.
Алгоритм работает пошагово – на каждом шаге он «посещает» одну вершину и пытается уменьшить метку вершины. Если все вершины посещены, алгоритм завершается.
Метка вершины 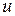 равна 0. В начале метки остальных вершин предполагаются равными +¥. Иначе, из ещё не посещённых вершин выбирается вершина
равна 0. В начале метки остальных вершин предполагаются равными +¥. Иначе, из ещё не посещённых вершин выбирается вершина 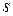 , имеющая минимальную метку. Рассматривают всевозможные маршруты с началом
, имеющая минимальную метку. Рассматривают всевозможные маршруты с началом 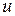 , в которых
, в которых 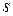 является предпоследним пунктом.
является предпоследним пунктом.
Для каждой не посещённой вершины 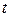 , смежной с вершиной
, смежной с вершиной 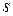 , находят сумму значения текущей метки
, находят сумму значения текущей метки 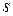 и веса ребра, соединяющего
и веса ребра, соединяющего 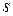 и
и 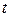 . Если полученная сумма s меньше значения t метки
. Если полученная сумма s меньше значения t метки 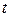 , то метку t заменяют меткой s.
, то метку t заменяют меткой s.
Рассмотрев все не посещённые вершины, смежные с вершиной 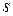 , вершина
, вершина 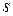 отмечается как посещенная, и повторяется шаг алгоритма.
отмечается как посещенная, и повторяется шаг алгоритма.
 2015-05-10
2015-05-10 199
199








