Пусть
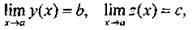 (11)
(11)
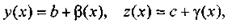 тогда на основании теоремы 2.1
тогда на основании теоремы 2.1
(12)
где 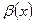 и
и 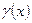 - бесконечно малые функции при х
- бесконечно малые функции при х 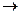 а.
а.
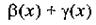
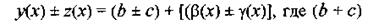 Принимая во внимание равенства (12), получаем
Принимая во внимание равенства (12), получаем
- постоянная - бесконечно малая функция при х 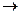 а.
а.
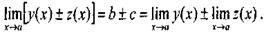 Согласно теореме 2.1 из последнего равенства следует, что
Согласно теореме 2.1 из последнего равенства следует, что
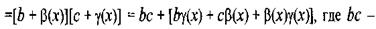
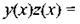 Поскольку
Поскольку
постоянная;
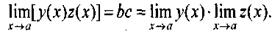
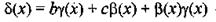 -бесконечно малая при х
-бесконечно малая при х 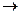 а, то на основании теоремы 2.1 получаем
а, то на основании теоремы 2.1 получаем
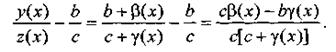 Предположив, что
Предположив, что 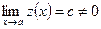 , составим разность
, составим разность
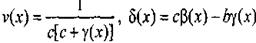 |
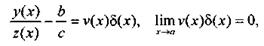 Обозначив получим
Обозначив получим
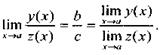 так как
так как 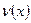 - ограниченная функция, а
- ограниченная функция, а 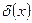 - бесконечно малая при х
- бесконечно малая при х 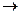 а. Следовательно,
а. Следовательно,
Следствие1. Если каждое слагаемое алгебраической суммы функций имеет предел при х 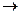 а, то предел суммы существует и равен такой же алгебраической сумме пределов слагаемых.
а, то предел суммы существует и равен такой же алгебраической сумме пределов слагаемых.
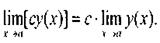 Следствие2. Постоянный множитель можно выносить я знак предела:
Следствие2. Постоянный множитель можно выносить я знак предела:
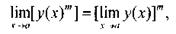 Следствие 3. Если
Следствие 3. Если 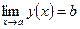 и т - натуральное число, то
и т - натуральное число, то
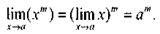 в частности,
в частности,
Теорема 3.3
Пусть три функции и = и(х), у = у(х), v= v(x) определены в некотором промежутке, содержащем точку а.
Если для любого х из этого промежутка выполняются неравенства
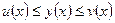 (13)
(13)
и функции и = и(х), v = v(x) имеют одинаковые пределы при х 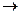 а, то функция у = у(х) имеет тот же предел при х
а, то функция у = у(х) имеет тот же предел при х 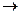 а.
а.
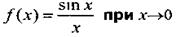 |
 2015-05-20
2015-05-20 247
247








