2015-05-20
186
Функция у = у(х), определенная на интервале (а, b), называется прерывной в точке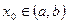 
,если
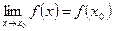(16)
(т. е. предел функции равен ее значению при предельном значении аргумента).
Согласно определению предела функции условие (16) равносильно следующему: для любого числа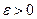 
существует такое число 
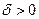, что при всех x, удовлетворяющих условию 
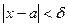, выполняется неравенство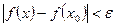 
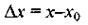
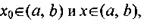Если то разность
называется приращение аргумента в точке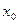 
а разность
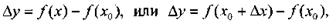
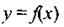приращением функции в той же точке.
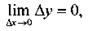
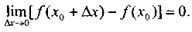Необходимое и достаточное условие непрерывности функции в точке х0 выражается равенством: или
Итак, функция непрерывна в точке, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции.
