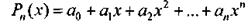Теорема 5.1

Если функци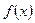и и 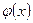непрерывны в точке х₀, то также не­прерывны в этой точке их сумма 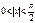+ 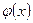, разность 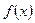- 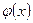, произведение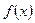 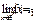, а также частное 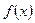/ 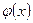при условии, что .

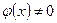Следствие 1. Целая рациональная функция

непрерывна при всех х.

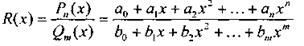Следствие 2. Дробная рациональная функция

непрерывна при всех х, для которых знаменатель не обращается в нуль.