Основные теоремы о пределах функций

Теорема 3.1

Функция у=у(х) не может иметь более одного предела при х 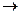а

Доказательство.

Предположим противное, пусть функция у=у(х) при х 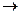а име­ет два предела b₁ и b₂: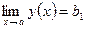 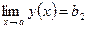, причем b₁ 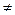b₂.

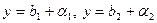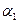Согласно теореме 2.1 из этих равенств следует, что , где и 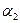- бесконечно малые, поэтому 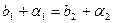, или 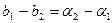. Последнее равенство невозможно, так как в левой части стоит постоянная, отличная от нуля, в правой - бесконечно ма­лая функция.

Теорема 3.2

Если каждая из функций у = у(х), z = z(х) имеет предел при х 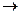а, то сумма, разность и произведение этих функций также име­ют пределы, причем

(8)

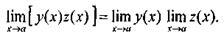(9)

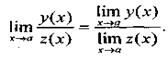Если, кроме того, 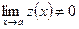, то и частное у(х):z(х) имеет предел, причем

(10)