Предел функции. Данная функция не определена только в точке х = 0, так как числитель и знаменатель в ней равны нулю

Данная функция не определена только в точке х = 0, так как числитель и знаменатель в ней равны нулю.

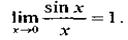Докажем, что эта функция имеет предел пр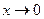и и

(14)

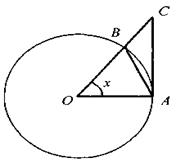
Рассмотрим окружность радиуса R, радианную меру цен­трального угла AОВ обозначим через х будем считать, что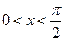

Поскольку площадь треугольника АОВ меньше площади сектора АОВ, а последняя меньше площади треугольника АОС (АС - каса­тельная к окружности в точке А) то

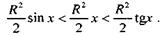
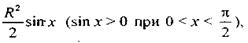Разделив эти неравенства на получим

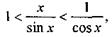
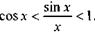
или (15)

Неравенства (15) в силу четности входящих в них функций верны не только для положительных, но и отрицательных х таких, что .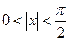

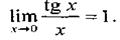Обращаясь к неравенствам (15), заключаем, что функция 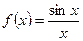удовлетворяет условиям теоремы 3.3. Согласно этой теореме получаем равенство (14), которое и требовалось доказать.

Замечание: