Проверка статистических гипотез

На разных стадиях статистического исследования часто возникает необходимость в экспериментальной проверке некоторых предположений (гипотез). Например, необходимо убедиться, что измеряемые величины нормально распределены. Наша цель состоит в том, чтобы проверить, не противоречит ли высказанное предположение (гипотеза) имеющимся выборочным данным.

Для количественного сопоставления эмпирического (статистического) и теоретического распределений или иными словами для того, чтобы принять или отвергнуть ту или иную статистическую гипотезу, используют результаты наблюдений. Пусть n наблюдений представлены последовательностью х ₁, х ₂, …, х_n. Тогда для проверки статистической гипотезы все пространство наблюдений разделяют на два непересекающихся подмножества R_{n 1} и R_{n 2}, т.е. R_{n 1} ∩ R_{n 2} = 0. Проверяемую гипотезу принимают по результатам наблюдений, если выборочная точка последовательности (х ₁, х ₂, …, х_n) попадает в область R_{n 1,} и отвергают при попадании этой точки в подмножество R_{n 2}, которая носит название критической. Выбор этой области однозначно определяет и область R_{n 1}.

Статистическая гипотеза характеризует поведение наблюдаемых признаков и является утверждением о параметрах распределения исследуемого признака (например, о среднем, дисперсии и т.д.). Такая гипотеза называется параметрической. Гипотеза о характере вида распределения случайной величины называется непараметрической.

Правило, по которому применяется или отклоняется выдвинутая гипотеза, называется статистическим критерием. Процедура обоснованного сопоставления высказанной статистической гипотезы с имеющимися в нашем распоряжении выборочными данными осуществляется с помощью того или иного статистического критерия и называется проверкой статистических гипотез.

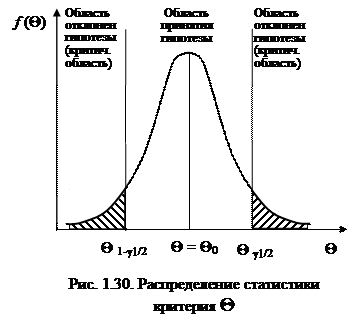
Правило, по которому строится тот или иной статистический критерий, состоит в том, что выбирается некоторая функция f (Q) = F (х ₁, х ₂, …, х_n), которая является мерой расхождения между измеренными и предполагаемыми теоретическими значениями исследуемой величины. Эта функция является случайной величиной и называется статистикой критерия. Закон распределения статистики критерия Q позволяет с заданной вероятностью принять или отклонить выдвинутую гипотезу.

Особый интерес представляет простой случай, когда среди параметров распределения случайной величины неизвестным является один, причем этот параметр может принимать лишь два конкретных значения Q₀ и Q₁.

Пусть Q₀ желаемое (″хорошее″) значение параметра Q, а Q₁ – не желаемое (″плохое″) значение. Задача формулируется как проверка гипотезы о том, что Q = Q₀. При проверке статистических гипотез эта выдвигаемая гипотеза обычно обозначается Н ₀(нулевая гипотеза). Тогда гипотезу о том, что Q = Q₁ называют конкурирующей (альтернативной) и обозначают Н ₁.

При проверке гипотезы Н ₀ против Н ₁ возможны два рода ошибок. Ошибка первого рода – это ошибка, когда отвергается верная гипотеза Н ₀. Ошибка второго рода – это ошибка, когда принимается неверная гипотеза Н ₁.

Вероятность ошибки первого рода обозначим g₁ = Р (отвергается Н ₀ | верна Н ₀). Символически можно записать в следующем виде:

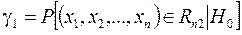, (1.69а)

т.е. вероятность ошибки 1-го рода g₁ есть вероятность принадлежности искомой выборки критической области R_{n 2} при условии истинности рассматриваемой гипотезы Н ₀.

Ошибку второго рода обозначим g₂(принимается Н ₀ | верна Н ₁). Ошибка второго рода с вероятностью g₂ состоит в том, что принимается неверная гипотеза Н ₀, в то время как в действительности верна конкурирующая гипотеза Н ₁, что символически записывается в виде:

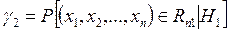, (1.69б)

т.е. вероятность ошибки 2-го рода g₂ есть вероятность принадлежности искомой выборки области допустимых значений R_{n 1}, при условии истинности конкурирующей гипотезы Н₁. Величину 1 - g₁,т.е.вероятность того, что гипотеза Н ₀будет отвергнута, когда она ошибочна, называют мощностью критерия и обозначают p.

В литературе величину g₁ иногда называют риском изготовителя, а величину g₂ - риском заказчика или потребителя.

Ошибку 1-го рода по аналогии с ошибкой при определении доверительного интервала называют уровнем значимости, тогда величина 1–g₁ будет доверительной вероятностью, т.е.

.

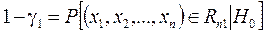Доверительная вероятность - это вероятность не совершить ошибку и принять верную гипотезу Н ₀. Вероятность отвергнуть ложную гипотезу Н ₀ называют мощностью критерия, т.е.

.

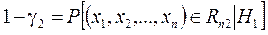Альтернативная гипотеза может принимать различные значения в зависимости от существа решаемых задач. Рассматриваемую как функцию от произвольного значения Q вероятность отвержения нулевой гипотезы, когда справедлива альтернативная Q₁, называют функцией мощности критерия.

Чем больше мощность критерия, тем меньше вероятность совершения ошибки второго рода g₂. Во всех случаях мощность критерия увеличивается при увеличении объема выборки.

В заданном объеме выборки невозможно одновременно сделать g₁ и g₂ сколь угодно малыми, поэтому, выбрав тем или иным способом критическую область g₁,находят критическую областьR_{n 2}, для которой величина ошибки g₂принимает минимальное значение.

Различают простые и сложные гипотезы. Статистическая гипотеза называется простой, если она однозначно определяет распределение исследуемого признака, в противном случае гипотеза называется сложной. Например, простой гипотезой является утверждение о том, что изучаемый признак X имеет нормальный закон распределения со средним значением, равным нулю, и единичной дисперсией. Если же высказывается предположение, что наблюдаемый признак X имеет нормальное распределение (не указываются при этом конкретные значения среднего и дисперсии или указывается значение только одного параметра), то это сложная гипотеза.

Распределение статистики критерия Q позволяет найти области принятия и отклонения гипотез. Задавая критические значения Q_1-g1/2 и Q_g1/2 (рис. 1.30), получаем области отклонения гипотезы (критические области). Точки Q_1-g1/2 и Q_g1/2 назы­вают критическими точками или квантилями, а интервал меж­ду ними – интерквантильным. Величина g₁ является уровнем значимости критерия и обычно выбирается достаточно малой. Наиболее часто задают величину g₁ = 0,1¸0,001. На рис. 1.30 величина g₁ равна сумме заштрихованных площадей.

Рассмотрим часто при­ме­няемый критерий согласия c²(критерий Пирсона)для проверки стати­сти­ческих ги­потез. Суть этого кри­терия состоит в следующем. Пусть нужно проверить гипо­тезу Н _0,состоящуюв том, что ре­зультаты наблюдений об­ра­зу­ют выборку из n значений Х – слу­чайной величины, которая име­ет некоторое заданное тео­ре­тическое распределение. Ста­вит­ся задача – определить, на­ско­лько близко выборочное рас­пределение случайной вели­чи­ны к ее теоретическому рас­пре­делению.

Для решения этой задачи все пространство значений наблюдаемой величины разобьем на непересе­каю­щи­еся области S ₁, S ₂, …, S_k. Обозначим через P_i вероятности попадания (при заданном распределении) в области S_i, а через m_i – число попавших в эти области наблюдений (частоты).

По данным наблюдений и с учетом теоретического распределения случайной величины определим

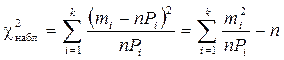. (1.70)

Величину f=k -1 называют числом степеней свободы, где k – число сравниваемых частот (разрядов). При 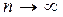плотность распределения величины χ² выражается соотношением

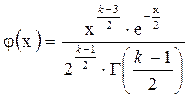. (1.71)

На практике при применении критерия согласия χ²пространство выборок разбивают не менее чем на пять непересекающихся областей S_k (k ³5), а число реализаций, попавших в область, должно быть не менее десяти. Для χ²-распределения вычислены таблицы вероятностей 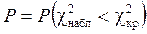(табл. П2). При использовании таблицы следует иметь в виду следующее. Если в качестве теоретического распределения задано однопараметрическое распределение, то берут число степеней свободы, равное f = k – 1.Если задано много­пара­мет­ри­чес­кое распределение, то число степеней свободы принимают равным f = k – p – 1, где p – число неизвестных параметров.

По значению 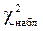,вычисленному по формуле (1.71), и известному числу степеней свободы f,используя табл. П2 находят P. Если значение P близко к единице, т.е. 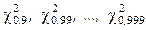, то вероятность того, что 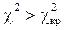мала, и, следовательно, гипотезу Н ₀нужно отбросить.

Для применения критерия χ² применяют метод, когда полученные данные группируют по интервалам частот и сравнивают с ожидаемым числом наблюдений для принятого распределения. На основе этого сравнения вычисляют критерий, который приближенно следует χ² - распределению только в том случае, если модель выбрана правильно. Если модель выбрана неправильно, то значение критерия превысит значение случайной величины, распределенной по закону χ². Для оценки правильности принятой модели используют численные значения процентилей 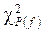– распределения, приведенные в табл. П.2.

Критерий Пирсона вычисляют по формуле:

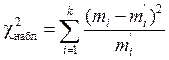, (1.72)

где k - число сравниваемых частот; m_i и m_i' - эмпирическая и теоретическая частоты в i -м интервале.

Полученные статистические данные делят таким образом, чтобы в каждый интервал попадало не менее пяти наблюдений. Если в каком-либо интервале число наблюдений окажется меньше пяти, то его объединяют с соседним интервалом таким образом, чтобы ожидаемое число наблюдений в объединенном интервале было не менее пяти.

Расчет значений 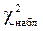удобно выполнять в форме табл. 1.6. После заполнения всей таблицы вычисляется число степеней свободы:

f = k – p – 1,

где k – число сравниваемых частот (в нашем примере k = 7); p – число параметров теоретического распределения (для нормального закона p = 2). В нашем примере f = 7 – 2 – 1 = 4.

Область допустимых значений критерия χ² или область принятия гипотезы характеризуются неравенством:

χ²_набл < χ²_кр (g₁, f),

где χ²_набл – значение критерия, вычисленное по данным наблюдений; χ²_кр(g₁, f) – критические значения критерия при заданных g₁ и f; g₁ – уровень значимости в технике, обычно принимается равным 0,05.

По табл. П2 находим χ²_кр (0,05; 8) = 15,5. Так как 5,88 < 15,5, то гипотеза о нормальном распределении анализируемой погрешности справедлива.

Используя метод разбиения на интервалы, можно определить вероятность попадания случайного наблюдения в i -й интервал из соотношения

Таблица 1.6

Вычисление критерия Пирсона

Номер интервала	mi	mi'	| mi – mi'|	| mi – mi'| 2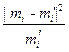
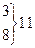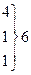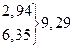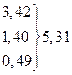	}	13,48 18,80 25,88 30,17 30,59 26,63 19,92 14,79 7,06	1,71 2,48 1,20 1,12 5,83 1,59 8,63 2,92 2,21 0,94 0,69	2,9241 6,1504 1,4400 1,2544 33,9889 2,5281 74,4769 8,5264 4,8841 0,8836 0,4761	0,31 0,46 0,08 0,05 1,13 0,08 2,80 0,43 0,33 0,12 0,09
Сумма					5,88

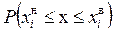
, i = 1, 2, …, k, (1.73)

где 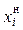- нижняя граница i -го интервала; 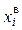- верхняя граница i -го интервала; k – число интервалов.

Границы интервала х ₁, х ₂, …, х_k определяют с помощью теоретического распределения с использованием следующих оценок параметров:

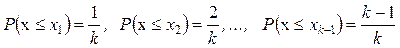, (1.74)

нижняя граница первого интервала и верхняя граница последнего интервала являются соответственно наименьшим и наибольшим значениями, которые может принимать случайная величина. Границы интервалов установлены таким образом, что для каждого интервала вероятность попадания случайной величины в него оценивается как 1/ k.

Математическое ожидание М _{х i} числа наблюдений в каждом интервале для принятой теоретической модели определяют:

М_хi = N / k, i = 1, 2, …, k. (1.75)

Подсчитывают число наблюдений в каждом интервале m_i и вычисляют критерий

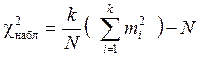. (1.76)

Сравнивают вычисленное значение 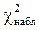с табличным значением для заданного уровня значимости и числа степеней свободы. Если вычисленное значение 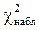превышает его табличное значение для a = 0,95,то вероятность того, что полученные данные имеют принятое распределение, не превышает 0,05, и модель отвергают как не удовлетворяющую требованиям.

Кроме того, можно пользоваться критерием Романовского:

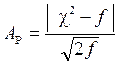. (1.77)

Если А _Р < 3, гипотеза принимается. Если А _Р > 3, гипотеза отвергается.

В нашем случае 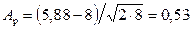, следовательно, эмпирическое распределение соответствует нормальному закону.

Если теоретические значения параметров известны, то лучшим является критерий Колмогорова λ_к

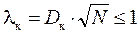, (1.78)

где 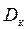– наибольшее отклонение теоретической кривой распределения от экспериментальной; N – общее количество экспериментальных точек.

При неизвестных параметрах этот критерий также применим, но в этом случае дает несколько завышенные оценки.

Применение данного критерия рассмотрим на примере, представленном в табл. 1.7.

В колонках 4 и 5 табл. 1.7 приведены накопленные суммы, которые образуются путем прибавления последующих частот к сумме предыдущих. Затем составляется разность между накопленными теоретическими и накопленными эмпирическими суммами (колонка 6) и находится максимальное значение этой разности. В данном примере она равна 7,38.

После этого находим

D _max = 7,38/ N = 7,38/200 = 0,037, N = ∑ m_i = 200.

Коэффициент λ_к находится по формуле

λ_к = D _max 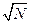= 0,036∙ 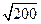= 0,50904.

Пример 1.6. В процессе испытаний десяти генераторов были зафиксированы следующие значения наработок между отказами, выраженные в часах: 2, 4, 4, 5, 5, 5, 6, 8, 8, 10, 12, 12, 15, 15, 16, 16, 18, 18, 19, 20, 21, 21, 21, 21, 22, 22, 22, 22, 23, 23, 23, 23, 23, 24, 24, 24, 24, 24, 24, 24, 2, 3, 4, 4, 4, 4, 5, 5, 5, 6.

Испытания генераторов проводилось в течение t = 500 ч, при этом весь период разбит на пять интервалов. Первые десять реализаций зафиксированы на первом интервале (0, t ₁) = 100 ч, вторые десять реализаций зафиксированы на втором интервале (t ₁, t ₂) = 100 ч и т.д. В качестве теоретического распределения наработки между отказами принят экспоненциальный закон с параметрами потока отказов (параметром распределения на каждом участке, равном λ _i). Ставится задача – провести проверку соответствия статистических данных наработок между отказами теоретическому распределению с помощью критерия χ².

Решение. Для вычисления квантиля χ² – распределения воспользуемся формулой (1.70)

.

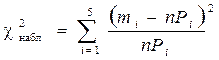Статистические данные разобьем на пять интервалов, и тогда в каждый интервал попадет по десять реализаций, т.е. m ₁ = m ₂ =…= m_i =10. Общее число реализаций в процессе испытаний равно: n = 50. Вероятность отказа на каждом участке (интервале) соответствует параметру интенсивности отказов на данном участке, который определяют по формуле

.

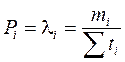Вычислим λ _i для каждого интервала:

;

;

;

;

.

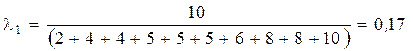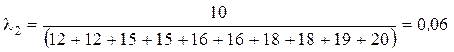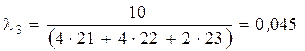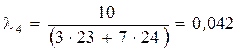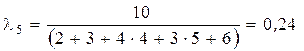Далее найдем значение :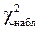

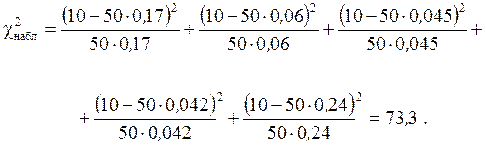
Принимая в качестве теоретического закона экспоненциальное распределение, найдем число степеней свободы: f = k – 1 = 5 – 1 = 4. Затем для числа степеней свободы f = 4 и квантиля 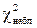= 73,3 по табл. П2 определим, что вероятность P > 0,999. Следовательно, гипотезу об экспоненциальном распределении для P >0,999 следует отбросить, так как χ 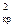(18,5) < 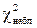(73,3).

Пример 1.7. По результатам эксплуатации двадцати приборов (n = 20)получены статистические данные о наработке до отказа каждого из них (табл. 1.9). На основе этих данных определить вероятность безотказной работы

Таблица 1.9

Время работы t_i до отказа каждого из 20 приборов

Номер интервала	ti, ч	Номер интервала	ti, ч	Номер интервала	ti, ч	Номер интервала	ti, ч

прибора за 10 ч, предполагая, что время безотказной работы распределено по экспоненциальному закону с помощью критерия χ².

Решение. Предположив экспоненциальный закон распределения времени работы прибора до отказа, найдем оценку параметра интенсивности отказа:

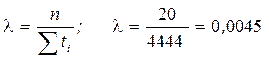1/ч.

Так как n = 20, то число интервалов выбираем равным n /5, поэтому k =20/5 = 4.

Для функции экспоненциального распределения 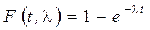находим границы интервалов, полагая

,

,

,

.

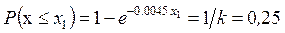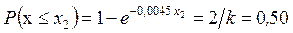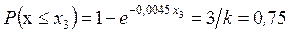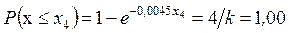Решая эти уравнения относительно x ₁, x ₂, x ₃, x ₄, находим интервалы:

, ,

, .

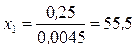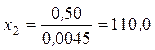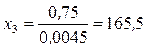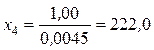Так как экспоненциально распределенная случайная величина при l = 0 изменяется от 0 до 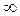, нижняя граница первого интервала равна нулю, а верхняя граница последнего интервала равна 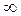. Вероятность попадания случайной величины в любой из интервалов равна 0,25. Исходя из данных табл. 1.5, примем x ₁ = 61; x ₂ = 152; x ₃ = 300 и составим таблицу (табл. 1.10).

Таблица 1.10

Сравнение фактических и ожидаемых данных, сгруппированных в интервалы

Интервал	Фактическое число mi наблюдений	Ожидаемое число Mx i наблюдений для выбранной модели
0 … 60,9 61 … 151,9 152 … 299,9 300 … 1200,0

Математическое ожидание числа наблюдений в интервале для принятой математической модели находят по формуле (1.75), оно составляет: M _{x i} = N / k = 20/4 = 5 для i = 1, 2, 3, 4. Фактическое число m_i наблюдений в i -м интервале находят непосредственно по исходным наблюдениям, приведенным в табл. 1.5. Сравнение величин m_i и M _{x i} дано в табл. 1.6.

Используя формулу (1.71), вычислим значение :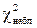

.

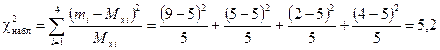Так как для экспоненциального распределения находили оценку одного параметра, то p = 1, поэтому число степеней свободы равно f = k – p – 1 = 4 – 1 – 1 = 2. По табл. П2 для двух степеней свободы находим

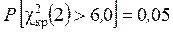или .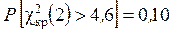

Следовательно, вероятность получить значение 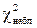= 5,2 для принятой теоретической модели заключена между 0,05 и 0,10. Таким образом, следует отвергнуть гипотезу об экспоненциальном законе распределения наработки прибора до отказа. Гипотеза об экспоненциальном законе распределения отвергается с вероятностью 0,9.