Признаки постоянства, возрастания и убывания функции

Рассмотрим функцию у = с, где с = const, сохраняющую одно и то же значение. Принимая во внимание следствие 1 из теоремы Лагранжа и формулу у' = 0, заключаем, что необходимое и достаточное условие постоянства функции выражается равенством

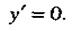
(3)

Введем определения возрастающей и убывающей функции.

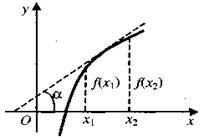
Функция у = называется возрастающей в некотором про­межутке (а, b), если для любых двух значени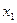й и 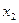, принадлежащих этому промежутку, из неравенства

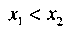(4)

следует неравенство

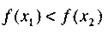(5)

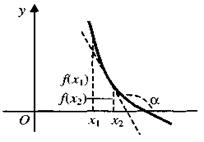
Функция у = называется убывающей в некотором проме­жутке, если для любых двух значений, принадлежащих этому проме­жутку, из неравенства (4) следует неравенство

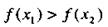(6)

Достаточное условие возрастания (убывания) функции выража­ется следующей теоремой.