2015-05-20
10865
Правило Лопиталя - Бернулли
При исследовании функций может появиться необходимость нахождения предела дроби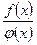 
, числитель и знаменатель которой при х—>а стремятся к нулю или бесконечности. Нахождение таких пределов называют раскрытием неопределенностей соответствующего вида. Основой его является правило Лопиталя - Бернулли, выражаемое следующей теоремой.
Теорема 1.1.
Если функции 
и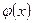 
дифференцируемы в окрестности точки х = а, обращаются в нуль в этой точке и существует предел отношения 
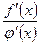при х—>а, то существует предел отношения самих функций, равный пределу отношения производных:
 |
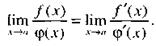(1)
Доказательство.
Пусть точка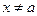 
принадлежит интервалу, в котором функции дифференцируемы. По теореме Коши
 |
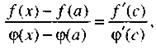где с лежит между х и а.
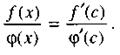По условию 
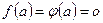, поэтому
Если х—>а, то и с—>а, так как с заключено между х и а. Переходя к пределу в последнем равенстве, получаем
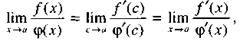откуда и следует формула (1).
