Теорема 2.1

Если в данном промежутке производная функции положитель­на, то функция возрастает в этом промежутке; если производная отрицательна, то функция убывает в соответствующем промежут­ке.

Доказательство.

Пусть 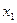и х ₂принадлежат промежутку, в котором 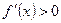; будем считать, что 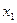< х ₂. По теореме Лагранжа

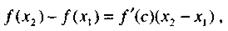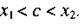(7)

где

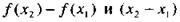
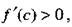Поскольку то разности одного знака, причем

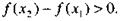
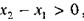поэтому

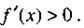
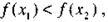
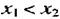Следовательно, из неравенства следует неравенство, т.е. функция возрастает в промежутке, где

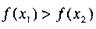
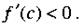
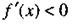Если для всех х из данного промежутка, то

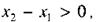
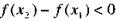Из неравенства (7) следует, что при т.е.

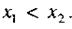когда

Это означает, что функция убывает в данном промежутке.