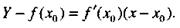Доказательство. Пусть функция у = такова, что >0 для всех x из проме­жутка (а, b)

Пусть функция у = такова, что 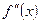>0 для всех x из проме­жутка (а, b). Фиксируем 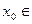(а, b), запишем уравнение касательной в этой точке, обозначив текущую координату через Y:

(11)

Разложим данную функцию в окрестности x ₀по формуле Тей­лора, приняв п = 2:

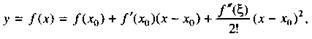(12)

где 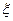лежит между х и х ₀.

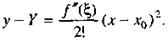Из формул (11) и (12) получаем

(13)

Поскольку (х-х ₀) 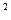> 0 и по условию 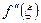> 0, то у - Y > 0, или у > Y.

Последнее неравенство означает, что график функции у = лежит выше касательной, проведенной в его произвольной точке М (х, ), где 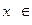(а, b). Следова­тельно, в промежутке (а, b) гра­фик функции у = является выпуклым вниз.

Аналогично доказывается второе утверждение теоремы.

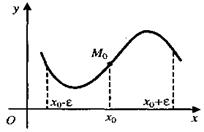Точкой перегиба графика функции у = называется такая его точка М₀, в которой выпуклость меняется на вогнутость (по отношению к одному и тому же направлению: вверх или вниз).