Многошаговые методы интегрирования

В многошаговых методах для получения решения дифференциального уравнения используются результаты нескольких предыдущих шагов интегрирования путем использования различных алгоритмов экстраполяции (extra - вне, pole - узел). Многошаговые методы позволяют сократить вычисления за счет использования результатов расчета предыдущих точек, но их недостаток в том, что они требуют «разгонки», т.е. первые шаги необходимо делать одним из одношаговых методов, что усложняет алгоритм. Другим недостатком многошаговых методов может служить их относительно меньшая устойчивость при интегрировании ОДУ, описывающих быстропеременные процессы, о чем будет сказано ниже.

В качестве примера рассмотрим современный многошаговый неявный метод ФДН, не требующий привлечения одношаговых методов для «разгонки», получивший распространение при расчете математических моделей в электротехнике, особенно в электромеханике при расчете процессов в электрических машинах.

Метод ФДН получил название от формулы записи аппроксимирующего интегрируемую функцию многочлена [7]:

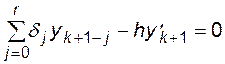, (4.19)

где r - порядок многочлена.

Соотношение (4.19) получило название формулы дифференцирования назад - ФДН. Как видно, в соотношении (4.19) присутствует производная искомой точки 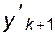, т.е. метод ФДН является неявным. Метод ФДН, как и другие неявные методы, достаточно сложен при программной реализации в сравнении с явными, требует больше оперативной памяти ЭВМ [8].

Как и все неявные методы, ФДН в общем случае для нахождения решения требует применения итерационных процедур с присущими им свойствами. Но, если производную удается представить в линейном виде 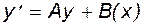, можно перейти к прямым способам поиска коэффициентов, входящих в формулы метода. Для многих задач электротехники это, как правило, имеет место (см. параграф 1.1, формулу (1.3) и параграф 4.1, формулу (4.3)).

Ниже приводятся основные соотношения, с помощью которых реализуется метод ФДН и его программная реализация для одного уравнения (ПРОГРАММА 4.3). Порядок метода r зависит от количества предшествующих рассчитываемой точке точек (узлов), информация о которых используется при расчете (рис 4.6).

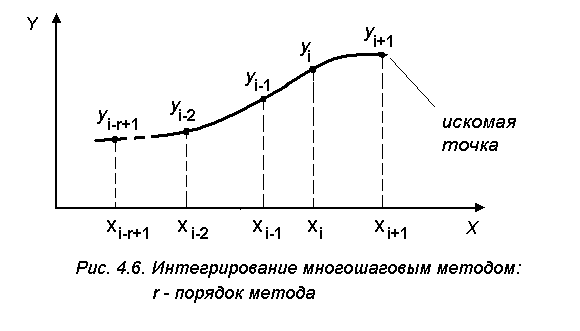
Если r= 1, то мы имеем одношаговый метод, известный как неявный метод Эйлера (см. параграф 4.3). Это может служить проверкой правильности программной реализации алгоритма метода ФДН.

Расчетная формула метода ФДН имеет вид

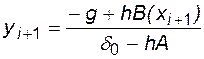, (4.20)

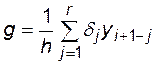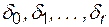где , а r+1 коэффициентов вычисляются из системы уравнений следующего вида:

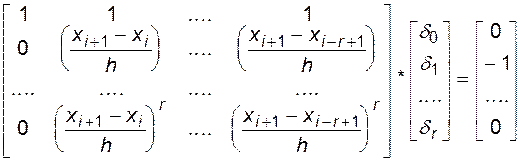. (4.21)

Система (4.21) относительно неизвестных 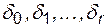решается методом Гаусса. Ниже (ПРОГРАММА 4.4) приведены процедуры расчета коэффициентов 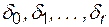и самого метода ФДН. При "разгонке" ФДН не нужно прибегать к другим методам интегрирования, нужно только, увеличивая порядок метода от 1 до принятого, пересчитывать коэффициенты 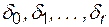. Пересчет их нужно вести и при изменении шага интегрирования h. Если и то и другое неизменно, расчет ведется по формуле (4.20) при постоянных параметрах.

Как и другие методы численного интегрирования, ФДН легко обобщается на системы дифференциальных уравнений.

Возможность оценки погрешности на шаге интегрирования (см. формулу(4.16)) позволяет автоматизировать выбор шага интегрирования как для явных, так и для неявных методов, и тем самым сократить время решения ОДУ [8].

Как говорилось ранее, неявные методы обладают большей устойчивостью при решении жестких уравнений. Дадим наглядное понятие о жестких ОДУ и об устойчивости решения ОДУ.