дифференциальных уравнений

Переходные процессы (см. главу 2) в электрических и электромеханических устройствах описываются с помощью систем дифференциальных уравнений. Их порядок определяется сложностью системы. В частном случае линейной электрической цепи, состоящей из активных сопротивлений и индуктивностей (R-L цепь), после исключения токов других ветвей, дифференциальное уравнение для тока k -й ветви будет иметь вид [4]:

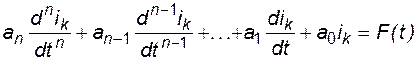, (4.22)

где n - число ветвей.

Уравнение (1.3) - его частный случай при n = 1. Система уравнений трансформатора (4.3) также сводится к уравнению (4.22), к уравнению второй степени, в чем можно убедиться самостоятельно, используя прием повторного дифференцирования [9].

Из курса математики известно, что полный интеграл дифференциального уравнения (4.22) состоит из частного решения, определяемого видом функции F(t), и полного решения однородного уравнения:

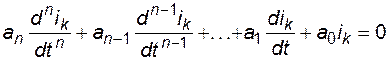. (4.23)

Для тока ветви i_k это обозначает, что он состоит из двух составляющих - 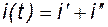, где 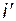называется принужденной составляющей, определяемой ЭДС после окончания переходного процесса, а 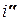- свободная составляющая, затухающая (по экспоненте для R-L цепи) во время переходного процесса.

В уравнении модели катушки электромагнита принужденная составляющая 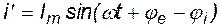, а свободная составляющая 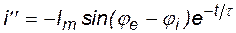, где 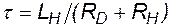- постоянная времени цепи.

При числе ветвей n свободная составляющая имеет вид:

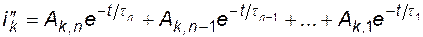. (4.24)

Свободные токи других ветвей также будут состоять из суммы экспонент с различной скоростью затухания, определяемой постоянными времени 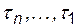при другой величине и знаках коэффициентов А.

При численном интегрировании уравнения (4.22) шаг h выбирают таким, чтобы он был соизмерим с наименьшей постоянной времени 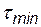. Для явного метода Эйлера это определяется следующим ограничением на шаг [6]:

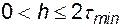. (4.25)

Если 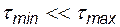, шаг интегрирования будет определяться наименьшей постоянной времени, а время расчета - наибольшей. Такие уравнения называются жесткими.

При численном интегрировании уравнение (4.22) заменяется системой из n уравнений первого порядка [1], и ее решение сводится к решению системы линейных алгебраических уравнений. Если исходная система дифференциальных уравнений жесткая, то матрица системы становится плохо обусловленной (см. пример в главе 1). Матрицу системы в связи с этим еще называют матрицей жесткости. Интегрирование такой системы при шаге больше граничного приводит к неустойчивости, быстрому накоплению погрешностей и аварийному завершению интегрирования.

Примером жесткой системы дифференциальных уравнений могут служить уравнения трансформатора (4.2) c матрицей системы L, у которого 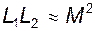, где L₁ и L₂ - индуктивности обмоток, М - коэффициент взаимоиндукции. Причем L₁ L₂ в реальном трансформаторе всегда больше М². Соотношение 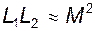имеет место в промышленных трансформаторах большой мощности. Легко убедиться, что определитель матрицы L в уравнении (4.2) равен L₁L₂-M², то есть при 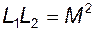он будет равен нулю и система не будет иметь решения.

Все методы интегрирования по влиянию шага h на устойчивость процесса интегрирования делятся на условно устойчивые и абсолютно устойчивые [6].Условно устойчивыми считаются методы, имеющие ограничение на максимальный шаг интегрирования h, абсолютно устойчивыми - не имеющие такого ограничения. Все явные методы относятся к условно устойчивым, среди неявных методов есть абсолютно устойчивые.

Подводя итог, можно сказать, что жесткость уравнений математической модели является свойством самого объекта исследования (электрической цепи, электрической машины, трансформатора), его параметров. При этом принято говорить о коэффициентной устойчивости. Скорость протекания процессов в системе зависит также и от скорости изменения воздействующих на нее внешних сил. В случае модели электромагнита замка это будет частота ЭДС источника.

При выборе шага интегрирования h следует иметь в виду, что шаг должен быть согласован как с параметрами математической модели, так и со скоростью изменения внешних сил, воздействующих на модель. Для электрических цепей ими являются ЭДС. Как отмечалось ранее, многошаговые методы при этом уступают одношаговым.

Для иллюстрации того, как влияют параметры модели и скорость протекания процесса, обусловленная приложенной ЭДС, на устойчивость и погрешность интегрирования различными методами, были проведены расчеты на модели электромагнита замка. Результаты расчетов приведены ниже. Шаг интегрирования h при исследовании влияния параметров модели на устойчивость процесса интегрирования принимался одинаковым и малым по сравнению с периодом ЭДС (T =40 h), чтобы погрешности интегрирования, связанные с изменением тока в результате действия ЭДС были минимальны. Для иллюстрации интегрирования быстро изменяющихся процессов многошаговыми и одношаговыми методами шаг выбирался соизмеримым с частотой питающей ЭДС, а постоянная времени 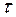- много большей, чем шаг ( 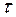=2500 h).

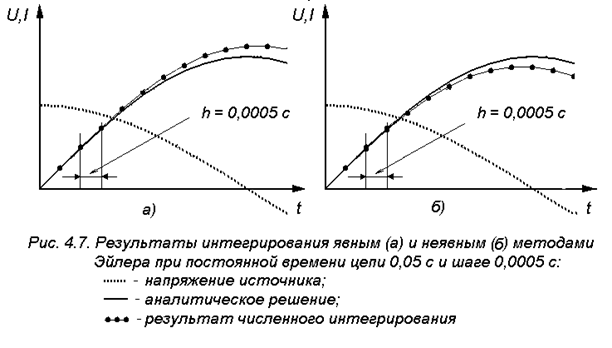
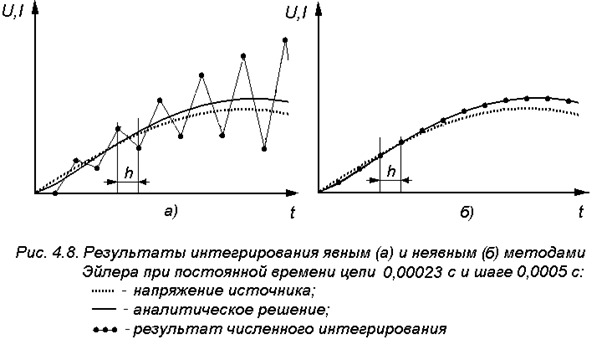
На рис.4.7 и 4.8 приведены результаты решения уравнения модели катушки электромагнита явным и неявным методами Эйлера при различных постоянных времени цепи катушки электромагнита.

При шаге h = 0.01 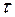(рис.4.7) оба метода дают одинаковую погрешность, но с разными знаками. При 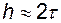(рис.4.8) явный метод становится неустойчивым, а неявный дает результат, близкий к аналитическому.

.

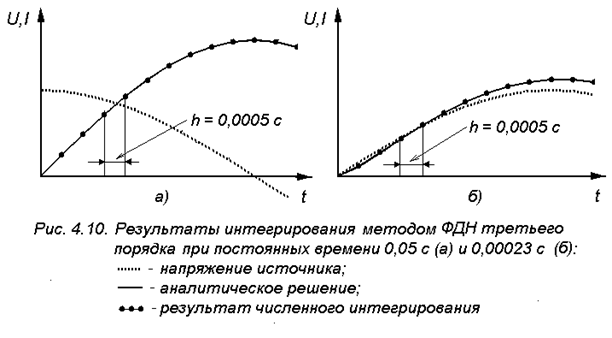
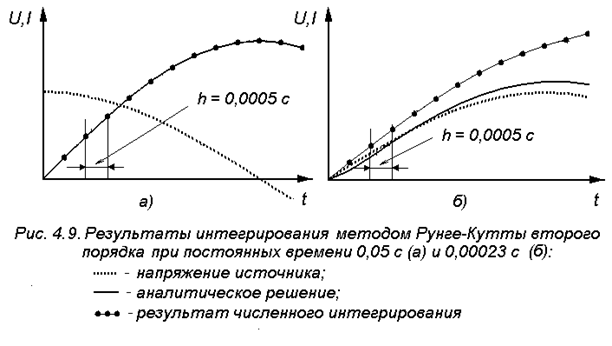
При интегрировании более точными методами Рунге- Кутты и ФДН с шагом h = 0.01 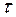получился результат практически совпадающий с аналитическим (рис.4.9,а и 4.10,а).

При шаге 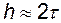расчет явным методом Рунге-Кутты ведется с возрастающей погрешностью, а неявным методом ФДН с той же точностью, что и с малым шагом по отношению к постоянной времени L_H/R_H (рис.4.9,б и 4.10,б).

. Анализируя сказанное выше, можно сделать следующий вывод. Шаг интегрирования системы ОДУ должен быть выбран так, чтобы быть соизмеримым с постоянной времени процесса, скорость которого в моделируемом устройстве будет максимальной.

Жесткой же называется система ОДУ, которая описывает одновременно протекающие динамические процессы, например в электрической цепи, скорости которых отличаются на несколько порядков.

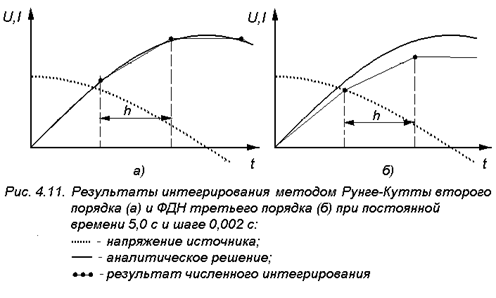
Скорость изменения интегрируемых величин - токов, напряжений и т.д. зависит не только от параметров объекта, но и от частоты действующих электродвижущих сил, и шаг интегрирования нужно выбирать, учитывая, что одношаговые методы при этих условиях точнее многошаговых. Примером могут служить графики на рис.4.11, где сравниваются методы Рунге - Кутты и ФДН.

Как видно из рисунка, при одинаковых условиях погрешность расчета методом ФДН получилась значительно выше.

Из сказанного выше можно сделать вывод о том, что не существует методов численного интегрирования, которые удовлетворяли бы всем условиям. Метод выбирается исходя из конкретной задачи, стоящей перед исследователем и возможностей ЭВМ (быстродействие, объем оперативной памяти). Для интегрирования уравнений систем, в которые входят электрические машины, следует отдавать предпочтение неявным методам.