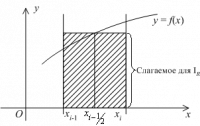
Рис.2
Заменим интеграл (3) выражением 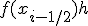 , где
, где 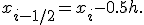
Тогда получим формулу
(5)
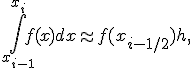
которая называется формулой прямоугольников на частичном отрезке 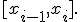
Погрешность метода (5) определяется величиной
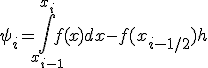
которую легко оценить с помощью формулы Тейлора. Действительно, запишем 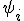 в виде
в виде
(6)
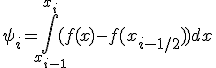
и воспользуемся разложением
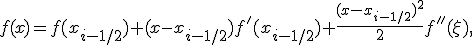
где 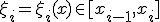 . Тогда из (6) получим
. Тогда из (6) получим
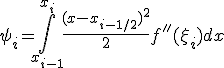
Обозначая 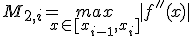 , оценим
, оценим 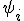 следующим образом:
следующим образом:
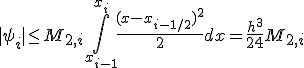
Таким образом, для погрешности формулы прямоугольников на частичном отрезке справедлива оценка
(7)
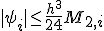
т.е. формула имеет погрешность 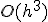 при
при 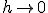 .
.
Заметим,что оценка (7) является неулучшаемой, т.е. существует функция 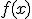 , для которой (7) выполняется со знаком равенства. Действительно, для
, для которой (7) выполняется со знаком равенства. Действительно, для 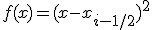 имеем
имеем 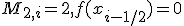 и
и
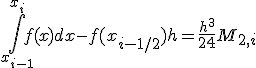
 2015-05-20
2015-05-20 407
407








