Решение с помощью подстановки у = u·v, где u = u(х) и v = v(х) — неизвестные функции от х, причем одна из них произвольна (но не равна нулю)
у(х) = 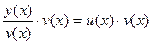 ,
,
где v(х) ≠ 0. Тогда у' = u'·v + v'·u. Подставляя выражения у и у' в уравнение (6), получаем:
u'·v + u·(v' + р(х)·v) = q(х) (7)
Подберем функцию v = v(х) так,чтобы выражение в скобках было равно нулю, т. е. решим ДУ v' + р(х)·v = 0. Т.о. 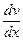 + р(х)·v = 0, т. е.
+ р(х)·v = 0, т. е. 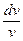 = – р(х)·dx.
= – р(х)·dx.
Интегрируя, получаем: 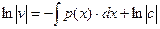
Ввиду свободы выбора функции v(х), можно принять с = 1.
Отсюда 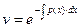
Подставляя найденную функцию v в уравнение (7), получаем 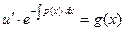
Получено уравнение с разделяющимися переменными. Найдем его решение:
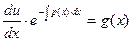 ,
, 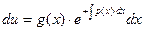 ;
; 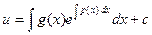
Возвращаясь к переменной у, получаем решение исходного ДУ.
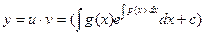
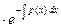 (8)
(8)
Пример 1. Проинтегрировать уравнение у' + 2х·у = 2х.
Решение: Пусть у = u·v. Тогда u'·v + v'·u = 2х· u·v = 2х, т.е. u'·v + u(v' + 2х·v) = 2х.
Сначала решаем уравнение v' + 2х·v = 0:
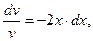
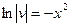 ,
, 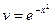
Теперь решаем уравнение 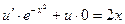 т.е.
т.е. 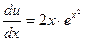 ,
, 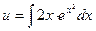 ,
, 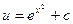 . Общее решение данного уравнения -
. Общее решение данного уравнения - 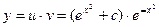 т.е.
т.е. 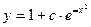
 2015-05-20
2015-05-20 394
394








