4.3.1. Ввести экспериментальные данные (xi, yi, i∊[0,n]).
4.3.2. Определить функциональные зависимости для аппроксимации экспериментальных данных на основе функций Mathcad, приведенных в таблице.
4.3.3. Вычислить в Mathcad значение коэффициента детерминации для каждой функциональной зависимости.
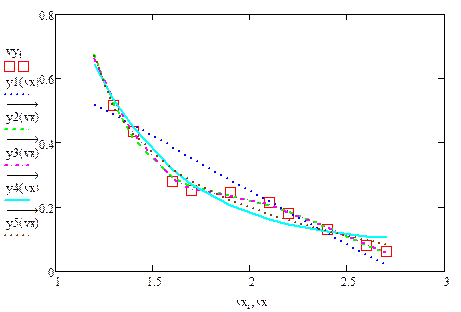
4.3.4. Отобразить графически в Mathcad исходные данные и полученные функциональные зависимости.
4.3.5. На основе вычисленных в Mathcad значений коэффициента детерминации обосновать выбор наилучшей функциональной зависимости. Для указанной функциональной зависимости, используя «Поиск решения» Microsoft Excel, определить значения коэффициентов этой функциональной зависимости, а затем сравнить их значения со значениями, полученных в Mathcad.
Пример
| Пример задачи |
| x | y | методы аппроксимации | «Поиск решения» |
| 1,2 | 0,6703 | Линейная Полиномиальная 4-ой степени Полиномиальная модель - loess (Фрагменты полиномов 2-ой степени) Логарифмическая Экспоненциальная | Экспоненциальная |
| 1,3 | 0,5169 |
| 1,4 | 0,4350 |
| 1,6 | 0,2800 |
| 1,7 | 0,2541 |
| 1,9 | 0,2466 |
| 2,1 | 0,2144 |
| 2,2 | 0,1809 |
| 2,4 | 0,1327 |
| 2,6 | 0,0821 |
| 2,7 | 0,0614 |
Для указанных экспериментальных данных определить указанные функциональные зависимости, рассчитать значения коэффициента детерминации и выбрать наилучшую функциональную зависимость. Для указанной функциональной зависимости, используя «Поиск решения» Microsoft Excel, определить значения коэффициентов этой функциональной зависимости, а затем сравнить их значения со значениями, полученных в Mathcad.
| Полиномеальная модель - loess |
Из приведенных расчетов можно сделать вывод, что наилучшей функцией является полиномиальная модель, полученная с помощью функции loess(), так как значение коэффициента детерминации для нее имеет максимальное значение = 0,998
Нахождение значений коэффициентов для экспоненциальной зависимости y(x)=a*eb*x+c с использованием блока «Поиск решения» приведено на листингах, расположенных ниже
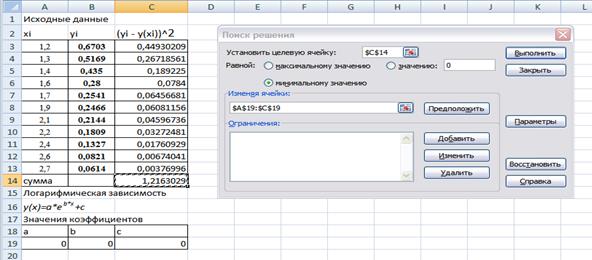
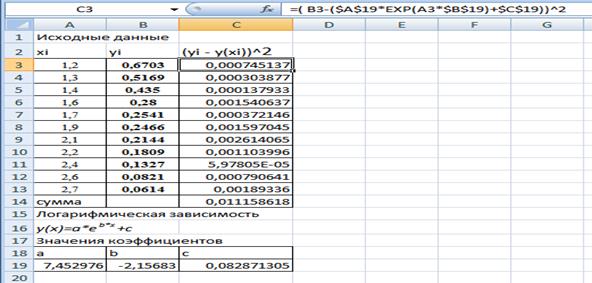
Как показывает анализ результатов, полученных в Mahcad и Excel, значения коэффициентов для экспоненциальной зависимости совпадают
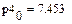
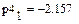
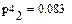
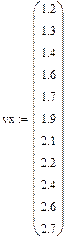
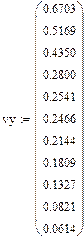
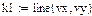
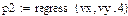
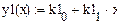
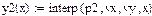
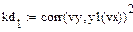
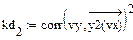
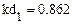
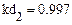
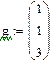
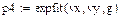
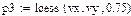
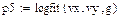
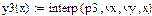
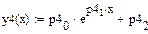
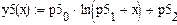
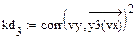
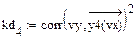
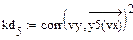
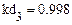
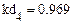
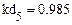
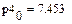
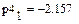
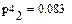
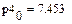
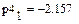
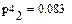


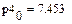
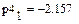
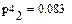
 2015-05-20
2015-05-20 1103
1103
