Лекция 14 Потоки событий и их свойства

Системы массового обслуживания. При исследовании различных информационных систем, связанных с предоставлением ресурсов, приходится сталкиваться с вопросами, относящимися к массовому обслуживанию. Характерной особенностью таких систем является наличие обслуживающей системы, в которую в случайные моменты времени поступают заявки. Обслуживающая система имеет линии (каналы), выполняющие совокупность операций, подразумеваемых под словом «обслуживание».

Потоки событий и их свойства. Заявки, поступающие в систему, образуют поток, т.е. последовательность событий, специальным образом распределённых во времени. Если с точки зрения обслуживания все заявки данного потока равноправны, то такой поток называется потоком однородных событий. Каждое событие потока в этом случае характеризуется только временем t_i, в которое оно наступает.

Чтобы описать случайный поток однородных событий как случайный процесс, достаточно знать закон распределения, характеризующий последовательность случайных величин t ₁, t ₂, …, t_m . В практических задачах моделирования удобнее вместо величин t ₁, t ₂, …, t_m рассматривать случайные величины ξ₁, ξ₂,..., ξ_m, являющиеся длинами интервалов времени между последовательными моментами t_j

t ₁ = ξ₁, t ₂ = ξ₁ + ξ₂, …, t_k = ξ₁ + ξ₂ + · · · + ξ _k.

Совокупность случайных величин ξ _j считается заданной, если определена совместная функция распределения

F (Z ₁, Z ₂, …, Z_k) = P (ξ₁ < Z ₁, …, ξ _j < Z_j, …, ξ _k < Z_k).

Обычно рассматривают только непрерывные случайные величины ξ _j, поэтому пользуются функцией плотности распределения

f (z ₁, …, z_j, …, z_k).

Для решения многих прикладных задач, связанных с массовым обслуживанием, можно ограничиться частными случаями потоков – потоками с ограниченным последействием, оперирование которыми оказывается более простым и доступным.

Случайный поток однородных событий называется потоком с ограниченным последействием, если случайные величины ξ _j являются независимыми. Очевидно, что для потоков с ограниченным последействием совместная функция плотности распределения f (z ₁, …, z_j, …, z_k) в соответствии с теоремой умножения теории вероятностей представляется в виде

f (z ₁, …, z_j, …, z_k) = f ₁ (z ₁) … f_j (z_j) … f_k (z_k).

Функции f_j (z_j) при j > 1 являются условными функциями плотности распределения величин ξ _j при условии, что в начальный момент интервала ξ _j (j > 1) в систему поступила заявка. В отличие от этого функция f ₁(z ₁) является безусловной функцией плотности распределения, так как относительно появления или не появления заявки в начальный момент времени не делается никаких предположений.

Большой теоретический и практический интерес представляют так называемые стационарные потоки, для которых вероятностный режим не зависит от начала отсчёта времени.

Более точно: поток однородных событий называется стационарным, если вероятность P_k (t, t ₀) появления K событий за промежуток времени [ t ₀, t ₀+ t ] не зависит от t ₀, а зависит только от t и K.

Для стационарных потоков с ограниченным последствием (потоков Пальма) имеет место соотношение

f ₂ (z ₂) = · · · = f_j (z_j) = · · · = f_k (z_k) = f (z).

Это значит, что при j > 1 интервалы ξ _j имеют одинаковые распределения вероятностей.

Стационарные потоки с ограниченным последействием характеризуются постоянной интенсивностью, или плотностью потока λ, имеющей смысл среднего количества событий, наступающих за единицу времени 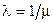, где µ – математическое ожидание случайной величины ξ _j при j > 1.

Для потоков Пальма имеет место соотношение, позволяющее определить f ₁ (z ₁), если известно f_j (z_j), j > 1 (формула Пальма)

.

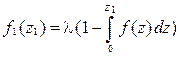Рассмотренные выше потоки являются ординарными. Поток событий называется ординарным, если вероятность попадания на элементарный участок 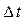двух и более событий пренебрежимо мала по сравнению с вероятностью попадания одного события.

В практике статистического моделирования приходится иметь дело с задачами, связанными с обслуживанием групповых заявок, создающих сгустки события, т.е. рассматривать неординарные потоки однородных событий. Для описания таких потоков, кроме моментов времени t_j, необходимо задать распределение количества заявок, поступающих в каждый из них.

Частным случаем потока Пальма является поток без последействия. Для такого потока закон распределения оставшейся части интервала времени между заявками не зависит от того, сколько этот интервал длится.

Поток называется простейшим, если он является стационарным, ординарным и потоком без последействия. Для простейшего потока вероятность P_k (t) наступления K событий за интервал времени длины t выражается законом распределения Пуассона

,

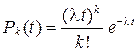поэтому часто простейший поток называют пуассоновским потоком. Из последнего соотношения следует, что функция плотности распределения f (z) случайной величины ξ _j при j > 1 для простейшего потока имеет вид показательного распределения с параметром λ, т.е.

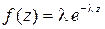
где λ – интенсивность потока.

В соответствии с формулой Пальма можно найти функцию плотности распределения f (z ₁) для первого интервала ξ₁:

.

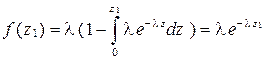Таким образом, в случае простейшего потока f ₁ (z ₁) = f (z). Это является особенностью простейшего потока. Для других потоков это равенство не выполняется.

Простейший поток играет среди потоков событий особую роль. Доказано, что при суммировании большого числа ординарных стационарных потоков с практически любым последействием получается поток, сколь угодно близкий к простейшему.