Сначала следует проделать с данными ту же процедуру присвоения рангов по каждому из вопросов, которая была описана при вычислении коэффициента Спирмена. В итоге получалась таблица:
| РАНГ по 1 вопросу | ||||||||
| РАНГ по 2 вопросу |
У нас есть N=8 пар рангов. Располагаем эти пары в порядке возрастанияранга по 1-му вопросу:
| РАНГ по 1 вопросу | ||||||||
| РАНГ по 2 вопросу |
Обратите внимание, что пары ответов не должны быть разбиты! например, рангу 6 по 1-му вопросу по-прежнему соответствует ранг 3 по 2-му вопросу.
Теперь вычисляем число инверсий по 2-му вопросу. Инверсией (для данного респондента) называется число рангов, превышающих ранг данного респондента и стоящих справа от него. Например, для ранга 2 справа оказались 6 рангов, больших 2: это 5,4,6,3,7 и 8. В итоге пполучаем таблицу:
| Число инверсий |
Суммируем число инверсий: 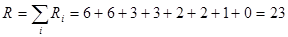
Коэффициент корреляции Кендалла вычисляется по формуле: 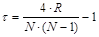
Вычисляем: 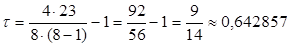 .
.
Значима ли величина коэффициента ранговой корреляции Кендалла?
Для этого требуется проверить гипотезу: «коэффициент ранговой корреляции Кендалла равен 0». Как и для коэффициента Спирмена, альтернативная гипотеза будет означать наличие значимой связи: «Коэффициент корреляции Кендалла отличен от 0».
Для проверки этой гипотезы нам потребуется использование функции Лапласа 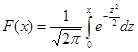 (о ней рассказывалось при изучении нормального распределения). Сначала мы, как и при проверке любой гипотезы, выбираем уровень значимости, например, α=0,05. Затем находим по таблице такой аргумент Zкрит, чтобы значение функции Лапласа F(Zкрит) было равно (1-α)/2. Сначала найдем, что
(о ней рассказывалось при изучении нормального распределения). Сначала мы, как и при проверке любой гипотезы, выбираем уровень значимости, например, α=0,05. Затем находим по таблице такой аргумент Zкрит, чтобы значение функции Лапласа F(Zкрит) было равно (1-α)/2. Сначала найдем, что 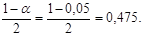 Затем по таблице подбираем такое значение, чтобы F(Zкрит)=0,475. Это значение Zкрит=1,96. Если Вы пользуетесь не справочниками, а Excel, имейте в виду, что функция обратного нормального распределения вычисляет интеграл Лапласа не от 0 до x, а от -∞.
Затем по таблице подбираем такое значение, чтобы F(Zкрит)=0,475. Это значение Zкрит=1,96. Если Вы пользуетесь не справочниками, а Excel, имейте в виду, что функция обратного нормального распределения вычисляет интеграл Лапласа не от 0 до x, а от -∞.
Найдя Zкрит, находим критическое значение коэффициента Кендалла τкрит по формуле 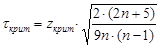 , или в нашем примере
, или в нашем примере
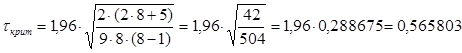
Осталось сравнить полученную величину коэффициента Кендалла с этим критическим значением. Поскольку экспериментальное значение 0,642857 больше, чем критическое значение 0,565803, мы отвергаем нулевую гипотезу и считаем, что коэффициент Кендалла в популяции не равен нулю, следовательно, между признаками существует связь. Тот же результат мы получили для данного примера и при использовании коэффициента Спирмена.
 2015-05-20
2015-05-20 5019
5019
