Проиллюстрируем статистическую проверку гипотез на примере следующей задачи. Для многих методов требуется, чтобы признаки, использующиеся в них, имели нормальное распределение. Простейшие критерии нормальности распределения (такие, как симметричность распределения, коэффициенты асимметрии и эксцесс) могут свидетельствовать о тех или иных отличиях распределения от нормального лишь приближенно. То, о чем будет рассказано ниже – это тоже приближенный метод, хотя и более точный. Дело в том, что нас интересует нормальность распределения во всей популяции, а нам известны лишь данные о некоторой выборке из этой популяции. Поскольку существует разброс, мы с некоторой вероятностью все равно можем получить такие экспериментальные данные, какие могли бы быть получены скорее при ненормальном распределении. Важно оценить по экспериментальным данным вероятность того, что мы получим такие экспериментальные данные, если распределение является нормальным.
Чтобы рассказ о проверке нормальности распределения был понятнее, разберем конкретный пример, взятый из классического учебника В. Е.Гмурмана (см. список литературы). Перед Вами данные, сгруппированные в виде частотной таблицы (например, пусть это будет производственный стаж работников определенной сферы):
| Интервал значений | Сколько в выборке таких значений |
| От 3 до 8 лет | |
| От 8 до 13 лет | |
| От 13 до 18 лет | |
| От 18 до 23 лет | |
| От 23 до 28 лет | |
| От 28 до 33 лет | |
| От 33 до 38 лет |
Сначала формулируем нулевую гипотезу, которую проверяем: «Распределение производственного стажа является нормальным». Альтернативная гипотеза будет сформулирована так: «распределение производственного стажа не является нормальным». Обратите внимание, что более конкретные гипотезы, например, «распределение является равномерным» не могут служить альтернативными к гипотезе о нормальном распределении, поскольку вместе основная и альтернативная гипотезы должны охватывать все возможные ситуации.
Для проверки того, является ли распределение нормальным, необходимо знать параметры этого распределения – среднее значение и стандартное отклонение. Иногда они известны заранее из других исследований. Тогда и основная гипотеза может быть сформулирована конкретнее, например: «Распределение является нормальным со средним значением 40 и стандартным отклонением 15». Но чаще всего эти параметры неизвестны, тогда их приходится сначала оценить по выборке. Как это сделать, было описано в начале пособия для различных типов группировки данных.
Если у нас данные уже сгруппированы в виде частотной таблицы, притом указаны границы интервалов, нам можно выбрать в качестве значения величины (в нашем примере – стажа) середину интервала, а потом воспользоваться формулами для вычисления среднего значения и стандартного отклонения. Так и сделаем.
| Левая граница xлев | Правая граница xправ | Середина xi | Сколько в выборке таких значений ni |
| 5,5 | |||
| 10,5 | |||
| 15,5 | |||
| 20,5 | |||
| 25,5 | |||
| 30,5 | |||
| 35,5 |
Всего в выборке 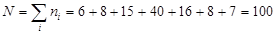 человек.
человек.
Среднее значение равно 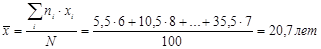
Дисперсия равна:
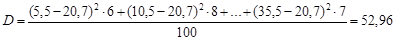
Стандартное отклонение равно 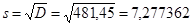 лет.
лет.
Следующие несколько шагов проверки нормальности распределения можно примерно описать так: весь диапазон значений исследуемой величины разобьем на несколько интервалов и посмотрим, сколько ответов попало бы в каждый из этих интервалов, если бы распределение действительно было нормальным. В той задаче, которая выбрана в качестве примера, разбиение на интервалы уже сделано (от 3 до 8, от 8 до 13 лет и т. д.). Если бы данные еще не были сгруппированы в виде частотной таблицы, границы интервалов пришлось бы выбрать сейчас, после чего подсчитать, сколько значений попало в какой из интервалов и таким образом все-таки преобразовать данные в частотную таблицу. Для того, чтобы проверка гипотезы работала наиболее эффективно, рекомендуется выбирать число интервалов так, чтобы в каждом из них оказалось хотя бы по несколько значений. Однако количество интервалов не должно быть очень маленьким – ведь по двум или трем интервалам трудно точно оценить форму распределения.
Для того, чтобы определять число значений, ожидаемое в каждом интервале, удобнее всего воспользоваться программой Excel, где значения функции нормального распределения можно вычислить с помощью функции НОРМРАСП (или в английской версии NORMDIST). Например, для левой границы 1-го интервала, равной 3, значение функции =НОРМРАСП(3;20.7;7.277362,ИСТИНА) равно 0,007504.
У функции НОРМРАСП четыре параметра: величина x, среднее значение, стандартное отклонение и некий логический параметр, который равен ИСТИНА, если требуется вычислить значение интегрального распределения (т.е.F(x)). Значением функции (результатом вычисления) будет вероятность того, что значение исследуемой величины окажется меньше указанного значения x, т.е. для нашего примера – то, что трудовой стаж меньше 3-х лет. Аналогично можно вычислить значения вероятностей для остальных границ. Вот они:
| Значение | Вероятность того, что величина примет меньшее значение |
| = НОРМРАСП(3;20.7;7,277362,ИСТИНА) = 0,007504 | |
| = НОРМРАСП(8;20.7;7,277362,ИСТИНА) = 0,04048 | |
| 0,14501 | |
| 0,355314 | |
| 0,624017 | |
| 0,842096 | |
| 0,954503 | |
| 0,991279 |
Вероятность попасть в интервал от 3 до 8 ищем, вычитая из вероятности принять значение <8 вероятность принять значение <3. И так делаем для всех интервалов. Эти вероятности представлены в следующей таблице (во 2-м столбце):
| Интервал значений | Вероятность попасть в данный интервал | Ожидаемая (теоретическая) частота | Измеренная частота | Разность частот |
| От 3 до 8 лет | 0,007504-0,04048 = 0,032977 | 3,2977 | 2,702027 | |
| От 8 до 13 лет | 0,10453 | 10,453 | -2,453 | |
| От 13 до 18 лет | 0,210303 | 21,0303 | -6,03033 | |
| От 18 до 23 лет | 0,268703 | 26,8703 | 13,12965 | |
| От 23 до 28 лет | 0,218079 | 21,8079 | -5,80791 | |
| От 28 до 33 лет | 0,112406 | 11,2406 | -3,24063 | |
| От 33 до 38 лет | 0,036776 | 3,6776 | 3,322404 |
В третьем столбце этой таблицы приведены ожидаемые (теоретические) частоты – сколько ответов ожидается в данном интервале, если распределение нормальное. Суть их вычисления следующая. В выборке 100 человек. В интервал от 3 до 8 лет значения любого из них попадут с вероятностью 0,032977. Если просуммировать всех, то в этом интервале окажется 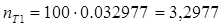 человека. Дробное значение числа респондентов не должно Вас смущать, поскольку реально значение теоретической частоты и не должно достигаться с большой точностью. В четвертом столбце для сравнения приведены значения измеренных частот: сколько ответов в каком интервале оказалось в нашем эксперименте. В последней колонке вычислены разности экспериментальных и теоретических частот, например, для интервала от 3 до 8 лет разность равна (n1-nт1) = 6 - 3,2977 = 2,702327.
человека. Дробное значение числа респондентов не должно Вас смущать, поскольку реально значение теоретической частоты и не должно достигаться с большой точностью. В четвертом столбце для сравнения приведены значения измеренных частот: сколько ответов в каком интервале оказалось в нашем эксперименте. В последней колонке вычислены разности экспериментальных и теоретических частот, например, для интервала от 3 до 8 лет разность равна (n1-nт1) = 6 - 3,2977 = 2,702327.
Понятно, что чем большие наблюдаются отклонения экспериментальных частот от теоретических, тем меньше экспериментальное распределение напоминает нормальное. Осталось получить некий статистический критерий – величину, свидетельствующую о том, можно ли принять гипотезу о нормальном распределении или ее следует отвергнуть. Такой величиной является величина хи-квадрат, равная по определению 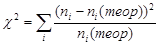 . Суммирование в этой величине происходит по всем интервалам. В качестве элементов суммы выступают квадраты разности экспериментальной и теоретической частоты, деленные на теоретическую частоту. В нашем примере значение χ2 равно:
. Суммирование в этой величине происходит по всем интервалам. В качестве элементов суммы выступают квадраты разности экспериментальной и теоретической частоты, деленные на теоретическую частоту. В нашем примере значение χ2 равно:
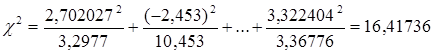
Теперь определим вероятность того, что в эксперименте, подобном нашему, получится такое (или большее) значение величины χ2. Математики получили, что если распределение величины в популяции является нормальным, то вычисленные подобным образом величины χ2 распределены по закону распределения хи-квадрат с числом степеней свободы, равным d=N-3, где N – число интервалов. В нашем случае имеется 7 интервалов, поэтому d=7-3=4.
Распределение хи-квадрат – это еще один вид распределения, часто использующийся в статистике. Математики создали для него таблицы (см. Приложение 3). В программе Excel имеется функция ХИ2РАСП (в английской версии CHIDIST) для вычисления по значению χ2 вероятности того, что это или большее значение χ2 получится в эксперименте. Эта вероятность носит название уровня значимости и обычно обозначается буквой α. Функция ХИ2РАСП имеет два параметра. Первый из них – значение хи-квадрат, второй – число степеней свободы. Воспользуемся функцией =ХИ2РАСП(16.41736;4) и получим α=0.002507. Данная величина означает, что если гипотеза верна и распределение является нормальным, то такие, как мы измерили, значения χ2 будут получаться лишь в 2,5 экспериментах из 1000 подобных нашему. Поэтому мы отвергаем гипотезу и считаем, что распределение нормальным не является. Какой уровень значимости считать достаточным для того, чтобы отвергнуть гипотезу, выбирает исследователь. Чаще всего считают, что распределение не является нормальным, если α<0,05.
Иногда проверку гипотезы делают в обратной последовательности. Сначала выбирается критический уровень значимости, меньше которого исследователь отвергнет гипотезу. Например, это может быть α=0,05. Затем по этому значению α и по известному числу степеней свободы (по-прежнему d=N-3=4) с помощью таблицы распределения хи-квадрат или с помощью функции ХИ2ОБР (в английской версии CHIINV) электронных таблиц Excel определяется критическое значение величины хи-квадрат. В нашем примере χ2 крит=ХИ2ОБР(0.05;4)=9.487729. Осталось сравнить экспериментальное значение χ2 с критическим значением. Если экспериментальное значение превышает критическое, то гипотезу о нормальном распределении отвергают и распределение не считают нормальным. Так, в рассмотренном нами примере экспериментальное значение χ2 =16,41736 больше, чем χ2 крит= 9,487729, и распределение не является нормальным.
Если компьютера под рукой нет, то приходится более сложно определять вероятности попадания исследуемой величины в интервалы, на которые мы разбили диапазон ее значений. Не имея Excel, можно воспользоваться таблицами функции нормального распределения, напечатанными в справочной и учебной литературе. Однако, эти таблицы, как правило, не приводятся для всех возможных средних значений и стандартных отклонений. В справочниках существуют таблицы функции Гаусса 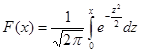 для среднего значения, равного 0 и стандартного отклонения s=1. Поэтому проверку приходится осуществлять для нормированной величины z. Разберем, как это делается, для нашего примера. У нас есть границы интервалов 3, 8, 13, 18 и т.д. Для каждой границы интервала xi получим его новое значение zi, вычитая среднее значение 20,7 и деля на стандартное отклонение 7,277. Например, для x1=3 значение
для среднего значения, равного 0 и стандартного отклонения s=1. Поэтому проверку приходится осуществлять для нормированной величины z. Разберем, как это делается, для нашего примера. У нас есть границы интервалов 3, 8, 13, 18 и т.д. Для каждой границы интервала xi получим его новое значение zi, вычитая среднее значение 20,7 и деля на стандартное отклонение 7,277. Например, для x1=3 значение 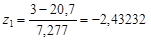 . Значение функции Гаусса для z1, найденное по таблице, равно 0,0075, как и получалось ранее. Напомню, что использовать таблицы, подобные приведенной в Приложении 2, для нахождения функции нормального распределения F(x) (с интегрированием не от 0, а от -∞) следует так:
. Значение функции Гаусса для z1, найденное по таблице, равно 0,0075, как и получалось ранее. Напомню, что использовать таблицы, подобные приведенной в Приложении 2, для нахождения функции нормального распределения F(x) (с интегрированием не от 0, а от -∞) следует так:
F(-2.43232)=0.5-Fтабл(2.43232)=0.5-0,4925=0,0075.
F(2,43232)=0.5+ Fтабл(2.43232)=0.5+0,4925=0,9925.
Для остальных границ величины вероятностей того, что случайная величина примет значения, меньшие данного, тоже совпадут с вычисленными ранее с помощью Excel. Поэтому дальнейшая проверка и ее результаты отличаться не будут.
В рассмотренном нами примере мы для простоты объяснения не учитывали тот факт, что интервалы, на которые была разбита выборка, охватывают не весь диапазон от 0 до бесконечности, а только от 3 до 38 лет. На полученный результат это не могло повлиять существенно, поскольку в неучтенные области события могли попасть с очень малой вероятностью (около 1%). Тем не менее, в таких случаях рекомендуется в качестве крайних интервалов использовать бесконечные. F(-∞)=0, F(∞)=1. Критерий хи-квадрат не требует равенства длин интервалов.
Для данной задачи требуется два признака, измеряемые по номинальной шкале. Требуется установить, есть ли связь между этими признаками в популяции. Данные некоторой анализируемой выборки (т.е. ответов респондентов) можно представить в виде таблицы сопряженности. Некоторые представления о том, как могут выглядеть данные, когда связь между признаками есть и когда эта связь отсутствует, были получены в предыдущем разделе. Однако не всегда данные интерпретируются так легко. К тому же, немалую роль играет статистика: ведь если в какую-либо ячейку в эксперименте попало 5 ответов, в другой раз может попасть 4 или 6 ответов. Изменится ли от этого интерпретация результатов? Иными словами, если мы получили в эксперименте указание на неодинаковое распределение (в процентах) между ответами на один из вопросов для разных вариантов ответа на другой вопрос, то значимо ли оно или вызвано лишь статистическим разбросом? Чтобы ответить на этот вопрос, требуется статистическая проверка гипотезы.
Нулевую гипотезу сформулируем так: «Признаки независимы». Альтернативная гипотеза – «между признаками существует связь». Метод проверки этой гипотезы покажем на примере, давая пояснения по ходу расчетов. Пусть респондентам задавали два вопроса: 1)Ваше семейное положение? (1-женат, 2-разведен, 3-не был женат), 2)Ваш род занятий? (1-рабочий, 2-крестьянин, 3-другое). Все ответы были сгруппированы в следующую таблицу сопряженности:
| женат | разведен | Не был женат | |
| Рабочий | |||
| Крестьянин | |||
| Другое |
Дополним данную таблицу суммами по строкам и по столбцам. То есть, вычислим, суммируя строки, общее число рабочих, крестьян и занимающихся другой деятельностью. Суммируя столбцы, вычислим число женатых, разведенных и тех, кто еще не был женат. В правом нижнем углу запишем общее число респондентов (просуммировав все ячейки). Получим такую таблицу:
| женат | разведен | не был женат | Всего | |
| Рабочий | 10+20+30=60 | |||
| Крестьянин | ||||
| Другое | ||||
| Всего: | 10+30+10=50 | 50+70+80=200 |
Теперь подумаем, как бы выглядели наши данные, если бы связи не было, т.е. если бы гипотеза о независимости была бы верна. Тогда в любой строке пропорции (в процентах) между ответами были бы одинаковыми и соответствовали пропорциям в целом по выборке. В нашем примере эти пропорции были бы 50/200=25% для женатых, 70/200=35% разведенных и 80/200=40% для еще не женившихся. Тогда среди 60 рабочих оказалось бы 60·25%=15 женатых, 60·35%=21 разведенных и 60·40%=24 еще не женившихся респондентов. Среди 100 крестьян было бы 100·25%=25 женатых, и т.д. Проделав такую процедуру со всеми 9-ю категориями людей (со всеми клетками), мы получаем следующую таблицу:
| женат | разведен | не был женат | Всего | |
| Рабочий | 60·50/200=15 | 60·70/200=21 | ||
| Крестьянин | 100·50/200=25 | |||
| Другое | ||||
| Всего: |
Величины, которые мы только что вычислили и записали в ячейки таблицы, называются теоретическими частотами, т.е. частотами, ожидаемыми в случае верной гипотезы. В таблице показан более простой для запоминания способ из вычисления:
Теоретическая частота = (сумма по строке) · (сумма по столбцу) / (число респондентов).
В нашем примере ожидаемое число женатых рабочих равно числу рабочих, умноженному на число женатых и деленному на общее число человек в выборке. Получив теоретические частоты, можно сравнить их с экспериментальными данными. Например, женатых рабочих ожидалось 15, а в эксперименте было опрошено всего 10, т.е. на 5 человек меньше. Напротив, разведенных крестьян вместо ожидаемых 35 в выборке оказалось 40, т.е. на 5 больше. Разности экспериментальных и теоретических частот позволяют выявить категории, в которых отличие эксперимента от ожидаемых результатов наиболее значительны. Это может помочь при интерпретации результатов. Однако, «значительно» - еще не значит «значимо». Требуется установить, существенны ли отличия экспериментальных частот от теоретических по сравнению с неизбежным статистическим разбросом. Для этого вычисляют следующую величину, называемую, как и при проверке нормальности распределения, хи-квадрат:
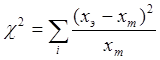
Здесь xэ – это экспериментальное значение частоты (число респондентов в i-й ячейке, полученное в эксперименте), а xт –теоретическая частота в этой ячейке. Суммирование проводится по всем ячейкам.
Удобнее всего вычисления оформлять в виде таблицы, где в ячейках будут величины 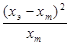 , а затем просуммировать все ячейки. В нашем примере таблица будет выглядеть так:
, а затем просуммировать все ячейки. В нашем примере таблица будет выглядеть так:
| женат | разведен | не был женат | |
| Рабочий | (15-10)2/15=1,666 | 0,0476 | 1,5 |
| Крестьянин | 0,7142 | 2,5 | |
| Другое | 1,1429 |
Таким образом, χ2 =1,666+0,0476+1,5+9+0,7142+2,5+0+1,1429+1=17,57143.
Дальнейшая проверка гипотезы о независимости стандартна. Выбираем уровень значимости гипотезы, например, α=0,05. Определяем число степеней свободы. Для данной задачи оно равно d=(число столбцов - 1)*(число строк - 1). В нашем примере d=(3-1)*(3-1)=2*2=4. По таблице распределения хи-квадрат с d=4 степенями свободы находим критическое значение хи-квадрат, равное в нашем примере χ2 =2,78. Поскольку экспериментальное значение χ2 =17,57143 больше критического, мы отвергаем нулевую гипотезу и считаем, что признаки «семейное положение» и «род занятий» связаны. Если бы выполнялось χ2 < χ2крит, мы бы приняли гипотезу о независимости признаков.
 2015-05-20
2015-05-20 4472
4472








