ЗЛП записана в форме стандартной задачи линейного программирования
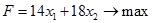
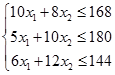
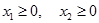
Для решения задачи симплекс-методом запишем ее в канонической форме:
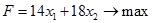
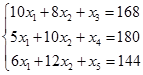
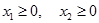
Составим начальную симплекс-таблицу
| Базис | 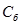 | 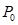 | 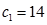 | 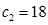 | 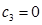 | 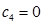 | 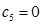 |
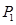 |  | 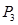 |  | 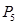 | |||
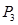 | |||||||
 | |||||||
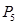 | |||||||
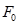 | 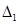 |  | 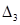 | 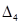 | 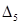 |
Последняя строка таблица определяется по формулам:
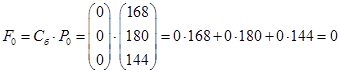
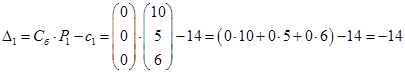
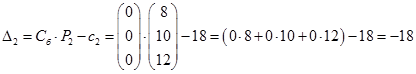
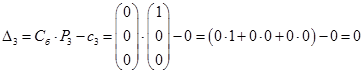
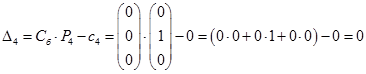
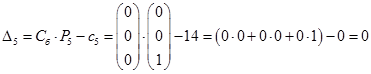
Таким образом, получим:
| Базис | 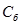 | 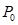 | |||||
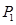 |  | 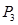 |  | 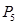 | |||
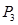 | |||||||
 | |||||||
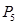 | |||||||
| -14 | -18 |
Так как последняя строка содержит отрицательные значения и соответствующие столбцы содержат положительные элементы, то план можно улучшить:
В качестве разрешающего столбца выберем столбец  , так как он содержит наибольшую по модулю отрицательную оценку. Для определения разрешающей строки найдем отношения элементов столбца
, так как он содержит наибольшую по модулю отрицательную оценку. Для определения разрешающей строки найдем отношения элементов столбца 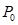 на соответствующие положительные элементы:
на соответствующие положительные элементы:
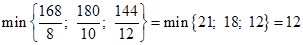
Таким образом, разрешающая строка – 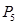 :
:
| Базис | 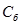 | 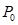 | |||||
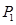 |  | 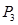 |  | 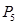 | |||
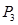 | |||||||
 | |||||||
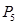 | |||||||
| -14 | -18 |
Построим новую симплекс-таблицу, заменив базисный вектор 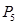 из разрешающей строки на ветор
из разрешающей строки на ветор  из разрешающего столбца:
из разрешающего столбца:
| Базис | 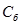 | 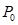 | |||||
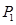 |  | 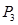 |  | 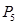 | |||
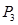 | |||||||
 | |||||||
 | |||||||
Так как вектор  заменил в базисе вектор
заменил в базисе вектор 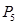 , то в новой таблице вектор
, то в новой таблице вектор  должен иметь вид
должен иметь вид 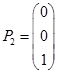 .
.
Разделив элементы разрешающей строки на разрешающий элемент (элемент на пересечении разрешающих строки и столбца) запишем в соответствующую строку новой таблицы:
| Базис | 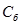 | 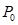 | |||||
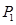 |  | 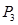 |  | 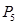 | |||
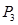 | |||||||
 | |||||||
 | 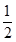 | 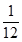 | |||||
Умножим полученную строку на (–8) и сложим с элементами строки, соответствующей вектору 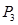 предыдущей таблицы:
предыдущей таблицы:
| Базис | 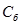 | 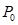 | |||||
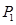 |  | 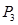 |  | 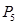 | |||
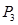 | 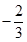 | ||||||
 | |||||||
 | 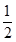 | 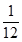 | |||||
Умножим полученную строку на (–10) и сложим с элементами строки, соответствующей вектору  первой симплекс-таблицы:
первой симплекс-таблицы:
| Базис | 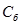 | 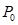 | |||||
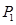 |  | 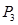 |  | 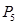 | |||
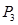 | 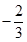 | ||||||
 | 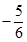 | ||||||
 | 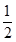 | 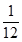 | |||||
Умножим полученную строку на (–10) и сложим с элементами строки оценок первой симплекс-таблицы:
| Базис | 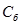 | 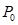 | |||||
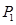 |  | 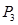 |  | 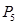 | |||
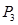 | 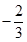 | ||||||
 | 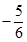 | ||||||
 | 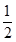 | 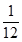 | |||||
| -5 | 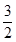 |
Так как строка оценок второй симплекс-таблицы содержит отрицательные элементы и соответствующий столбец содержит положительные элементы, то план можно улучшить.
Аналогично определяем разрешающий столбец и разрешающую строку:
| Базис | 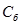 | 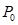 | 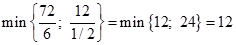 | |||||
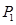 |  | 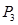 |  | 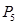 | ||||
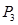 | 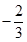 | |||||||
 | 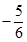 | |||||||
 | 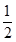 | 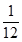 | ||||||
| -5 | 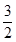 |
Построим третью симплекс-таблицу, аналогично предыдущей:
| Базис | 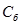 | 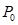 | |||||
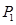 |  | 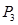 |  | 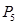 | |||
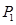 | 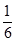 | 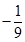 | |||||
 | 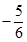 | ||||||
 | 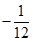 | 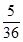 | |||||
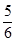 | 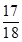 |
Так как последняя строка не содержит отрицательных оценок, то полученный план оптимален и имеет вид:
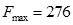 при плане
при плане 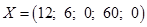
Ответ: 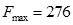 при плане
при плане 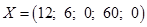
 2015-05-10
2015-05-10 1240
1240








