ЗЛП записана в форме стандартной задачи линейного программирования
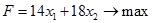
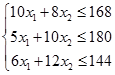
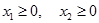
Для построения области допустимых решений преобразуем систему ограничений, выразив в каждом неравенстве переменную 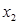 :
:
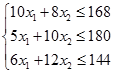 | 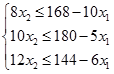 | 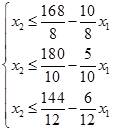 | 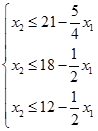 |
Построим на плоскости три прямые, уравнения которых получены из преобразованной системы ограничений заменой знака неравенства на знак равенства:
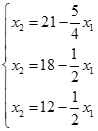
Прямая 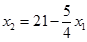 проходит через точки:
проходит через точки:
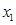 | 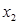 |
Прямая 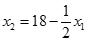 проходит через точки
проходит через точки
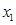 | 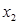 |
Прямая 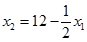 проходит через точки
проходит через точки
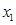 | 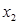 |
Построим прямые:
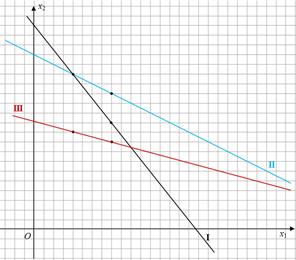
Каждое неравенство системы ограничений определяет полуплоскость:
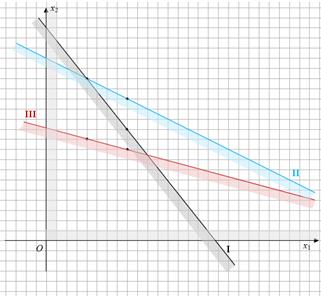
Пересечение полуплоскостей определяет область допустимых решений
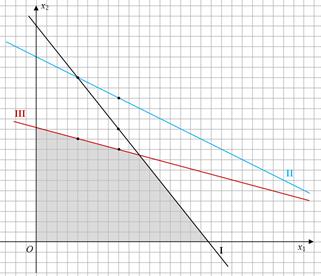
Построим вектор 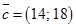 и линию уровня
и линию уровня 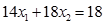

Так как необходимо определить максимум целевой функции, то передвигаем линию уровня параллельно самой себе в направлении, совпадающим с направлением вектора 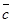 :
:
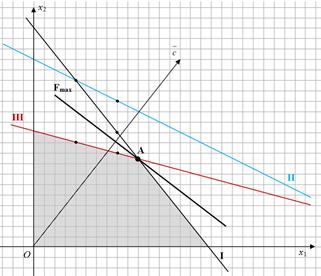
Таким образом, целевая функция достигает максимума в точке А, которая является точкой пересечения прямых I и III. Найдем координаты точки A, решив систему уравнений, составленную из уравнений прямых I и III:
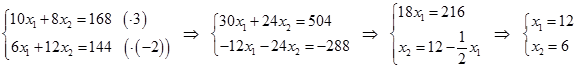
Найдем максимальное значение целевой функции 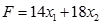 , подставив найденные значения для
, подставив найденные значения для 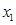 и
и 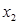
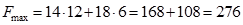
Таким образом, максимальная прибыль 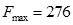 достигается при производстве 12 изделий вида
достигается при производстве 12 изделий вида 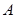 и 6 изделий вида
и 6 изделий вида 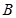 .
.
Ответ: 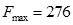 при плане
при плане 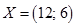
 2015-05-10
2015-05-10 879
879







