Пассивный двухполюсник в цепи переменного тока

Лабораторная работа №3

1. Цель работы:

Экспериментальная проверка и анализ основных положений теории линейных электрических цепей синусоидального тока.

2. Основные положения и соотношения:

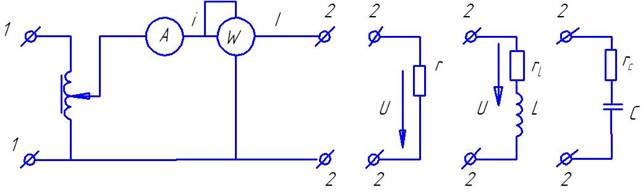
Для учета процесса преобразования электромагнитной энергии в схемы замещения цепей синусоидального тока вводят пассивные двухполюсные элементы: резистивный – r (рисунок 3.1.а), индуктивный - L (рисунок 3.1.б), емкостный – С (рисунок 3.1.в).

а) б) в)

Рисунок 3.1.

В цепи с активным сопротивлением r при синусоидальном напряжении 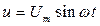ток 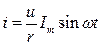совпадает по фазе с напряжением.

Мгновенная мощность

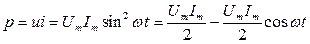
имеет постоянную составляющую, равную средней мощности за период, которая называется активной мощностью:

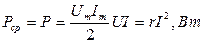
В цепи с индуктивностью L при напряжении

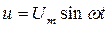
Ток 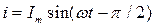отстает по фазе от напряжения на угол 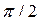, его амплитуда

,

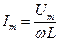где 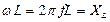- индуктивное сопротивление.

Мгновенная мощность

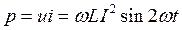
изменяется по синусоиде с двойной частотой 2ω.

Максимальное значение 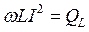называется индуктивной реактивной мощностью .

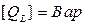В цепи с емкостью С при напряжении 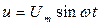ток 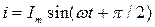опережает по фазе напряжение на угол 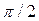, его амплитуда

,

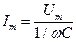где 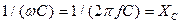- емкостное сопротивление.

Мгновенная мощность

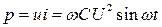
изменяется по синусоиде с двойной частотой.

Максимальное значение называется емкостной реактивной мощностью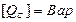

В цепи с последовательным соединением участков r, L, С (рисунок 3.2.) мгновенное значение приложенного напряжения:

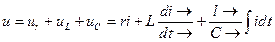(1)

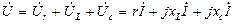(2)

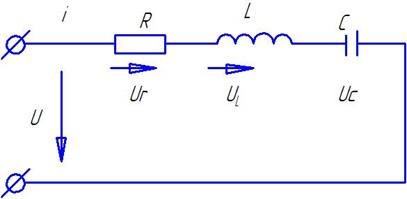
Рисунок 3.2.

Векторные диаграммы токов и напряжений исследуемой цепи (рисунок 3.2) приведены на рисунке 3.3:

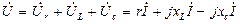
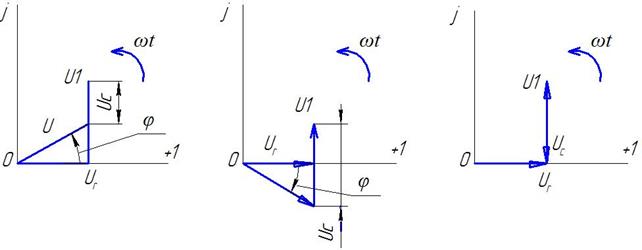
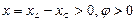
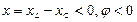
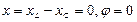
Рисунок 3.3

Полная мощность цепи:

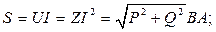(3)

где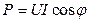

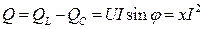
В цепи с параллельным соединением участков r, L, С: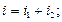
в комплексной форме

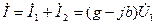(4)

где 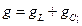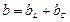(см. рисунок 3.4.).

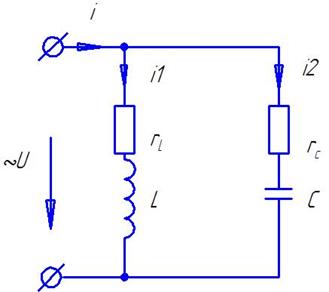
Рисунок 3.4.

Векторная диаграмма токов и напряжений:

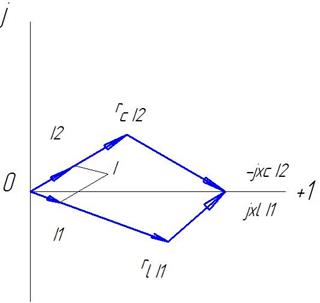
Рисунок 3.5.

На основании показаний амперметра (I), вольтметра (U) и ваттметра (Р) определяют:

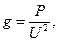
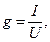
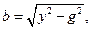
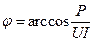(5),

а также могут быть рассчитаны теоретически, если известны сопротивления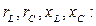

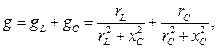
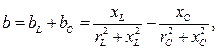
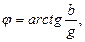(6)