Квадратурные формулы с равностоящими узлами

Квадратурные формулы с равностоящими узлами применяются для вычисления интеграла:

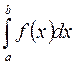
с постоянной весовой функцией и конечным отрезком интегрирования.

1.1.1. Квадратурная формула прямоугольников

Пусть на отрезке 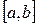задана функция 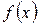. Введем сетку, разбивающую отрезок 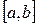на N равностоящих узлов.

где 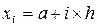, шаг 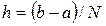и обозначим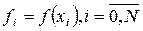

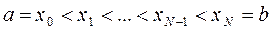
Выберем на каждом сегменте серединную точку 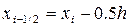и обозначим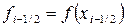

Квадратурная формула прямоугольников имеет вид:

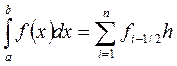
Если функции 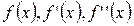непрерывны на отрезке 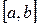, то остаточный член имеет вид:

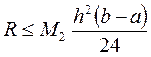, где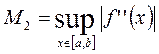

1.1.2. Квадратурная формула трапеций имеет вид:

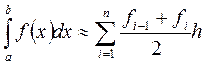
или

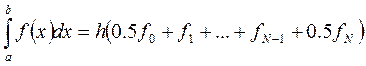
Если функции 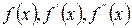непрерывны на 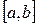, то остаточный член представляется в виде:

,

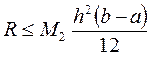где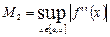

1.1.3. Квадратурная формула Симпсона

Выберем на каждом сегменте серединную точку 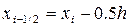и обозначим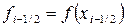

Квадратурная формула Симпсона имеет вид:

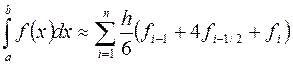
Также можно взять удвоенный частичный отрезок, обозначив 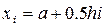, 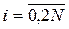и .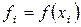

В результате получим другой вариант формулы Симпсона:

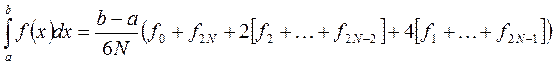
При этом, если функция 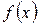имеет на отрезке 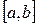непрерывные производные до четвертого порядка включительно, то остаточный член имеет вид:

,

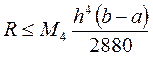где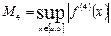

Решая неравенство 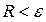относительно h для остаточных членов любой из квадратурных формул и делая вычисления с таким шагом, получаем заданную точность 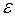вычисления.