2015-05-10
205
Пример 1:
Вычислить интеграл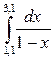 
по квадратурным формулам прямоугольников, трапеций и Симпсона, сравнить с точным значением интеграла и вычислить остаточный член для каждой формулы
Точное значение интеграла:
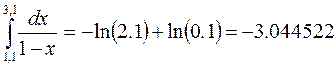
1. Квадратурная формула прямоугольников
Для вычисления интеграла введем сетку, разделяющую отрезок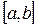 
на n=10 частей, при этом h=0,2. Выберем на каждом сегменте 
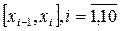срединную точку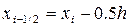 
Применяя квадратурную формулу прямоугольников получаем:
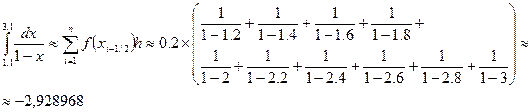
Оценим погрешность по общей формуле.
Поскольку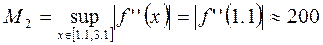 
,
то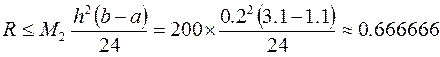 
При сравнении точного значения интеграла и полученного имеем разницу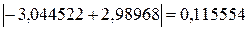 
. Сравнивая эту разницу с погрешностью, можно сказать, что оценка явно завышена.
2. Квадратурная формула трапеций.
Введем сетку также, как в пункте 1.
При этом h=0.2, N=10 по квадратурной формуле трапеции:
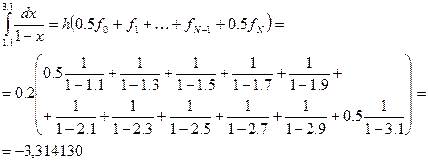
При этом оценка погрешности составляет:
При сравнении точного и полученного значения интеграла разность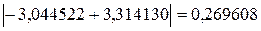 
значительно меньше погрешности 0,66666, что говорит о явно завышенной оценке.
3. Квадратурная формула Симпсона.
|
|
|
Введем сетку как в пункте 1. Пусть h=0.2, n=10.
Чтобы не использовать дробные индексы, обозначим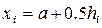 
, 
, 
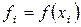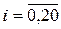и записываем формулу Симпсона в виде:
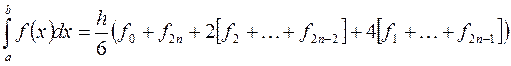
Вычислим интеграл по квадратурной формуле Симпсона:
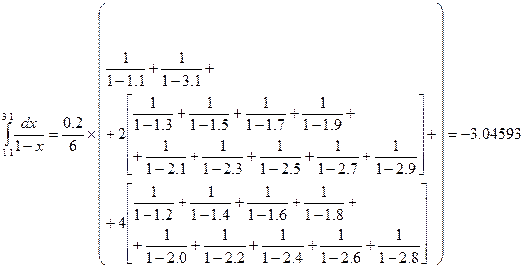
Оценка погрешности этой формулы:
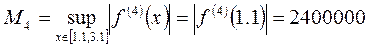
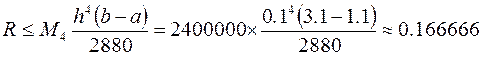
Сравнение точного значения интеграла с полученным дает разность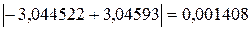 
. Эта разность меньше погрешности. Можно сказать, что в данном случае оценка также завышена.
Пример2:
Выбрать шаг интегрирования для вычисления интеграла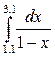 
с точностью 0,01 пользуясь квадратурными формулами прямоугольников, трапеций, Симпсона.
Оценку погрешности для каждой квадратурной формулы будем брать из примера 1 соответственно.
