Вычислим, при каком шаге h погрешность составит 0,01:
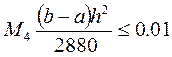
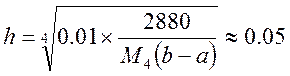
При шаге 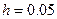 , отрезок
, отрезок 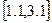 разбивается на N=40 равностоящих узлов.
разбивается на N=40 равностоящих узлов.
Как и следовало ожидать, наименьшее количество равностоящих узлов N=40 получается при вычислении интеграла по квадратурной формуле Симпсона.
Апостериорная оценка погрешности методом Рунге. Автоматический выбор шага интегрирования.
Пусть 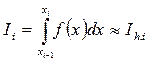 - квадратурная формула, примененная на частичном отрезке и имеющая порядок m, то есть
- квадратурная формула, примененная на частичном отрезке и имеющая порядок m, то есть 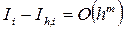 . Для формул прямоугольников и трапеций m = 3, а для формулы Симпсона m = 5. Проведем на каждом частичном отрезке
. Для формул прямоугольников и трапеций m = 3, а для формулы Симпсона m = 5. Проведем на каждом частичном отрезке 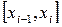 все вычисления дважды, один раз с шагом
все вычисления дважды, один раз с шагом 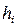 , другой раз с шагом
, другой раз с шагом 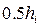 . Тогда справедлива оценка:
. Тогда справедлива оценка:
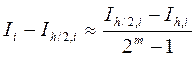
Если для заданного 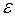 правая часть не превосходит
правая часть не превосходит  , то получим:
, то получим:
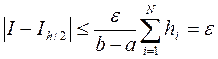
то есть будет достигнута заданная точность 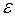 .
.
Если же на каком-то из частичных отрезков эта оценка не будет выполняться, то шаг на этом отрезке надо измельчить еще в два раза и снова оценить погрешность. Заметим, что для некоторых функций такое измельчение может продолжаться слишком долго. Поэтому в соответствующей программе следует предусмотреть ограничение сверху на число измельчений, а также возможность увеличения 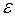 .
.
 2015-05-10
2015-05-10 304
304








