Вычислить приближенное значение интеграла с помощью формулы а) прямоугольников, б) трапеций, в) Симпсона. Величину шага выбрать заранее, сделав вручную оценку погрешности через вторую (случаи а,б) или четвертую (случай в) производные. Сравнить с точным значением интеграла
ВАРИАНТЫ ЗАДАНИЙ К ЛАБОРАТОРНОЙ РАБОТЕ 5
1.(а) 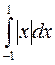 1.(б)
1.(б) 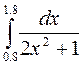 1.(в)
1.(в) 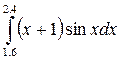
2.(а) 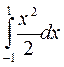 2.(б)
2.(б) 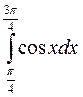 2.(в)
2.(в) 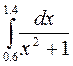
3.(а) 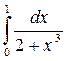 3.(б)
3.(б) 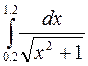 3.(в)
3.(в) 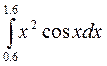
4.(а) 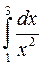 4.(б)
4.(б) 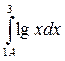 4.(в)
4.(в) 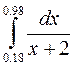
5.(а) 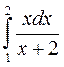 5.(б)
5.(б) 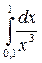 5.(в)
5.(в) 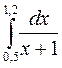
6.(а) 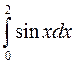 6.(б)
6.(б) 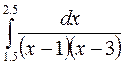 6.(в)
6.(в) 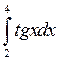
7.(а) 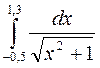 7.(б)
7.(б) 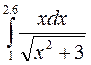 7.(в)
7.(в) 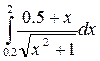
8.(а) 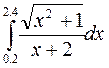 8.(б)
8.(б) 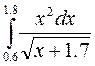 8.(в)
8.(в) 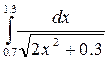
9.(а) 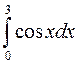 9.(б)
9.(б) 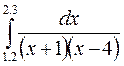 9.(в)
9.(в) 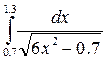
КОНТРОЛЬНЫЕ ВОПРОСЫ
- Какая формула называется квадратурной и почему?
- Запишите остаток квадратурной формулы
- В каком случае применяются квадратурные формулы с равностоящими узлами?
- Запишите и поясните квадратурную формулу прямоугольников
- Запишите и поясните квадратурную формулу трапеций
- Запишите и поясните квадратурную формулу Симпсона
- Как получается заданная точность вычисления?
ЛИТЕРАТУРА
1. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. М.: Высшая школа, 1994.
 2015-05-10
2015-05-10 307
307







