Дискретная случайная величина, характеризуемая законом распределения 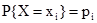 , может трактоваться как полная группа событий, если каждому из этих событий поставить в соответствие одно из возможных значений случайной величины. Поэтому моделирование дискретной случайной величины, заданной рядом распределения, не отличается от моделирования полной группы событий. Такой способ моделирования дискретной случайной величины называется стандартным. Кроме него для многих законов распределения существуют специальные алгоритмы, позволяющие более просто и «изящно» смоделировать случайную величину.
, может трактоваться как полная группа событий, если каждому из этих событий поставить в соответствие одно из возможных значений случайной величины. Поэтому моделирование дискретной случайной величины, заданной рядом распределения, не отличается от моделирования полной группы событий. Такой способ моделирования дискретной случайной величины называется стандартным. Кроме него для многих законов распределения существуют специальные алгоритмы, позволяющие более просто и «изящно» смоделировать случайную величину.
Наиболее важными дискретными случайными величинами являются целочисленные с законом распределения 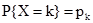 , k=0,1,2,... Среди них наибольшее применение при исследовании сложных технических систем находят распределения, связанные со схемой Бернулли (биномиальное, геометрическое, Паскалево, отрицательное биномиальное), а также распределение Пуассона.
, k=0,1,2,... Среди них наибольшее применение при исследовании сложных технических систем находят распределения, связанные со схемой Бернулли (биномиальное, геометрическое, Паскалево, отрицательное биномиальное), а также распределение Пуассона.
Биномиальная, геометрическая, Паскалева и отрицательная биномиальная случайные величины получаются из последовательности независимых испытаний Бернулли, если эту последовательность оборвать тем или иным способом, например, после n испытаний, или после k успехов. Примем следующую терминологию:
р - параметр испытания Бернулли (вероятность успеха в одном испытании);
n - число испытаний;
k - число успехов;
y - число неудач.
В соответствии с этим будем обозначать:
1. Биномиальную случайную величину - число успехов в n испытаниях - B(n,p), при этом
Р{В(n,p)=k}= pk= Cnk pk qn-k. (2.8)
2. Геометрическую случайную величину - число испытаний до первого успеха (включая первый успех) - G(p), при этом
Р{G(p)=n}= pn= p qn-1. (2.9)
3. Паскалеву случайную величину - число испытаний до k-го успеха (включая k-ый успех) - С(k,p), при этом
Р{С(k,p)=n}= pn= Cn-1n-k pk qn-k. (2.10)
4. Отрицательную биномиальную случайную величину - число неудач до k-го успеха - Y(k,p), при этом
Р{Y(k,p)=y}= py= Ck+y-1y pk qy. (2.11)
В зависимостях (2.8-2.11) q=1-p, 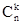 - число сочетаний из n по k.
- число сочетаний из n по k.
Распределение Пуассона (будем обозначать PS(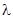 ) используют в том случае, когда число n независимых испытаний велико, а вероятность р успеха в каждом отдельном испытании мала. По сути распределение Пуассона является предельной формой биномиального распределения при n
) используют в том случае, когда число n независимых испытаний велико, а вероятность р успеха в каждом отдельном испытании мала. По сути распределение Пуассона является предельной формой биномиального распределения при n 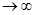 и р
и р 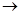 0. При этом
0. При этом
Р{PS(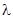 )=k}= pk=
)=k}= pk= 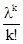 exp(-
exp(- 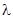 ), (2.12)
), (2.12)
где 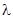 =np - параметр распределения Пуассона (математическое ожидание или, иначе говоря, среднее число успехов в n испытаниях).
=np - параметр распределения Пуассона (математическое ожидание или, иначе говоря, среднее число успехов в n испытаниях).
При выборе между биномиальной, отрицательной биномиальной или пуассоновской моделями можно руководствоваться следующими свойствами:
биномиальная: дисперсия < среднее;
отрицательная биномиальная: дисперсия > среднее;
Пуассона: дисперсия = среднее.
На практике широкое применение для моделирования СВ с биномиальным распределением получил метод браковки.
Введем случайную величину Хi - число успехов в i-ом испытании. Очевидно, что эта величина может принимать только два значения: либо 1 с вероятностью р, либо 0 с вероятностью 1-p, т.е. ряд распределения величины Хi такой:
| Xi | 1 0 |
| P | p 1-p |
Тогда случайное число успехов в n испытаниях можно представить в виде: k= X1+X2+...+Xn.
На основе этого можно построить следующий алгоритм моделирования B(n,p):
1. Получить последовательность чисел r1,r2,...,rn случайной величины R[0,1].
2. Для каждого числа проверить выполнение условия ri < p. При его выполнении Хi=1, в противном случае Хi=0.
3. Найти сумму n значений СВ Хi, которая и будет значением случайной величины B(n,p).
Математически данный алгоритм можно записать в виде:
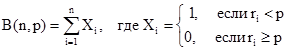 (2.13)
(2.13)
Наиболее применяемые алгоритмы моделирования указанных выше распределений приведены в таблице 2.1.
При решении практических задач, связанных с законом Пуассона, обычно задается параметр 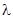 , а ни n, ни p неизвестны. В связи с этим алгоритм моделирования пуассоновской СВ, представленный в табл.2.1., учитывает данное обстоятельство и реализован методом браковки. При этом перед его применением необходимо выбрать n такое, чтобы р=
, а ни n, ни p неизвестны. В связи с этим алгоритм моделирования пуассоновской СВ, представленный в табл.2.1., учитывает данное обстоятельство и реализован методом браковки. При этом перед его применением необходимо выбрать n такое, чтобы р= 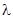 /n была достаточно малой (p < 0.01).
/n была достаточно малой (p < 0.01).
Таблица 2.1.
Моделирование дискретных случайных величин
| Распределение | Процедура моделирования |
| Биномиальное B(n,p) | 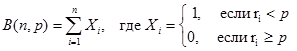 |
| Геометрическое G(p) | 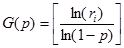 округление до целого в большую сторону округление до целого в большую сторону |
| Паскаля C(k,p) | 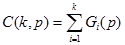 |
| Отрицательное Биномиальное Y(k,p) | 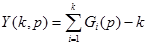 |
Пуассона PS(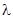 ) ) | PS(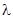 )= )= 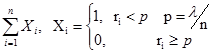 |
 2015-05-10
2015-05-10 778
778








