При моделировании непрерывных случайных величин применяют четыре основных метода:
- метод обратных функций (Смирнова);
- метод исключения (Неймана);
- метод суперпозиции;
- предельные теоремы теории вероятностей.
Составим алгоритм моделирования нормальной случайной величины, используя центральную предельную теорему для СВ, равномерно-распределенных на интервале [0,1].
Пусть r1,r2,...,rn - независимые СВ, равномерно-распределенные в интервале [0,1]. Обозначим через Y сумму этих величин:
Y = r1+r2+...+rn.
Применяя теоремы сложения математических ожиданий и дисперсий независимых случайных величин, получим:
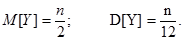
В силу центральной предельной теоремы можно считать, что Y имеет нормальный закон распределения с параметрами N(n/2; 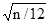 ).
).
Для дальнейшего изложения понадобится понятие стандартной случайной величины. Стандартной случайной величиной (Z) называется безразмерная центрированная СВ, у которой математическое ожидание равно нулю, а дисперсия 1:
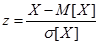 . (2.19)
. (2.19)
Действительно:
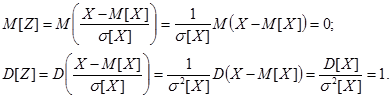
Перейдем от величины Y к стандартной нормальной случайной величине:
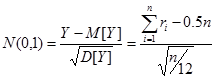 (2.20)
(2.20)
Таким образом, получили зависимость для моделирования стандартной нормальной случайной величины. Легко заметить, что зависимость (2.20) приобретает простой вид при n=12:
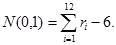 (2.21)
(2.21)
Принимая во внимание (2.19), нетрудно получить зависимость для моделирования нормальной случайной величины с заданными параметрами:
x = M[X] + 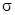 [X]×N(0,1). (2.22)
[X]×N(0,1). (2.22)
В настоящее время на основе зависимостей (2.21) и (2.22) строятся практически все алгоритмы моделирования нормальных СВ на ЭВМ.
Для наиболее часто встречающихся в практике исследований сложных военно-технических систем непрерывных случайных величин алгоритмы их моделирования представлены в табл.2.2.
Таблица 2.2.
Моделирование непрерывных случайных величин
| Распределение и его плотность | Процедура моделирования |
Равномерное R[a,b]
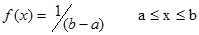
| 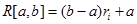
|
| Показательное EXP(l); l>0 f(x)=l exp(-lx) x>0 | EXP(l)=-(1/l)ln(1-ri) |
Рэлея RL(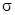 ) )
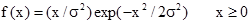
| RL(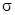 )= )= 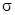 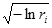
|
Вейбулла WB(a,b); a,b>0
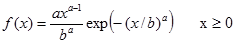
| WB(a,b)=b(-lnri)1/a |
Стандартное нормальное N(0,1)
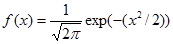
| N(0,1)= 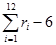
|
Нормальное N(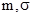 ) )
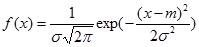
| N(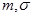 )=m+sN(0,1) )=m+sN(0,1)
|
Логнормальное LN(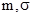 ); ); 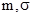 >0 >0
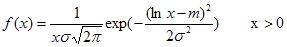
| LN(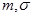 )=exp(m+sN(0,1)) )=exp(m+sN(0,1))
|
Гамма-распределение GM(a,b)
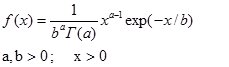
| 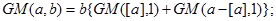
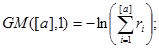
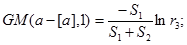
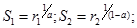 см. примечание.
см. примечание.
|
Примечание: Для генерации GM(a-[a],1) используется следующий метод: вычисляются S1 и S2 , если S1+S2 >1, то берется следующая пара r1 и r2 до тех пор, пока не выполнится условие S1+S2 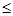 1. Генерация СВ, имеющих гамма-распределение, основано на методе суперпозиции.
1. Генерация СВ, имеющих гамма-распределение, основано на методе суперпозиции.
 2015-05-10
2015-05-10 570
570








