Параметрический тест Голдфельда – Квандта

При малом объеме выборки для оценки гетероскедастичности можно использовать метод Голдфельда – Квандта. Метод разработан в 1965 году на линейной модели, для которой дисперсия остатков возрастает пропорционально квадрату фактора.

Проверяется нулевая гипотеза 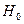об отсутствии гетероскедастичности остатков. Конкурирующая гипотеза 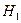– наличие гетероскедастичности остатков.

1.Упорядочить 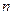наблюдений по мере возрастания переменной .

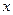2.Исключить из рассмотрения 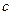центральных наблюдений. При этом 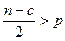, где 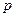– число оцениваемых параметров.

3.Построить по каждой из двух разделенных групп из 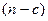наблюдений с малыми и большими значениями фактора уравнений регрессии.

4.Определить остаточные суммы квадратов для первой 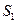и второй 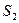групп (или по «урезанным выборкам»).

5.Найти наблюдаемое значение критерия .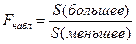

6.Сравнить наблюдаемое значение критерия с табличным .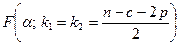

7.Сделать вывод: нулевая гипотеза 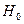принимается на уровне значимости 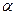, если .

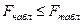Для случая одного фактора рекомендовано при количестве данных 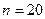принимать 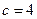, при 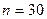принимать 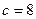, а при – .

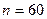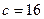Тест Голдфельда – Квандта применяется в том случае, если ошибки регрессии можно считать нормально распределенными случайными величинами. Критерий Голдфельда – Квандта используется и при проверке остатков множественной регрессии на гетероскедастичность. При обнаружении гетероскедастичности остатков ставится цель ее устранения, чему служит применение обобщенного метода наименьших квадратов (ОМНК). ОМНК применяется к преобразованным данным и позволяет получить оценки, которые обладают не только свойством несмещенности, но и имеют наименьшие выборочные дисперсии.

ПОСТАНОВКА ЗАДАЧИ

Для статистических данных, представленных в таблице согласно вашему варианту, проверьте наличие гетероскедастичности, используя тест Голдфелда-Квандта на уровне значимости 0,05.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Введите исходные данные.

2. Расположите 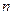наблюдений по мере возрастания переменной 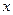. Для этого на панели инструментов Стандартная щелкните по кнопке Сортировка по возрастанию.

3. Исключите из рассмотрения примерно 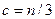центральных наблюдений. При этом должно выполняться условие .

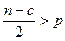4. Определите остаточные суммы квадратов, то есть суммы квадратов остатков регрессии по «урезанным выборкам»:

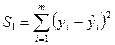и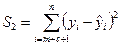

Вычислите остаточные суммы квадратов средствами Excel. Сначала найдите остаточные суммы квадратов первой выборки.

4.1. Выделите область пустых клеток (5×2), в которой вы хотите разместить таблицу с регрессионными параметрами.

4.2. В главном меню выберите Вставка/функция.

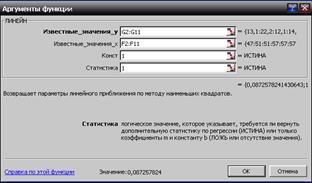
4.3. В окне Категория выберите Статистические, затем в окне Функция – ЛИНЕЙН. Заполните диалоговое окно.

Входные данные

Известные значения 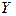– диапазон (столбец), содержащий данные результативного признака выборки 1.

Известные значения 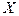– диапазон (столбец), содержащий данные факторов независимого признака выборки 1.

Константа – 1.

Статистика – 1.

4.5. Нажмите ОК. В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы.

4.6. Для раскрытия таблицы данных нажмите F2, затем вместе клавиши «ctrl-shift-enter».

Регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:

Значение коэффициента	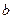Значение коэффициента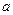
Стандартная ошибка	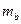Стандартная ошибка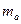
Индекс детерминации	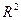Среднеквадратическое отклонение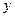
F- статистика	Число степеней свободы
Регрессионная сумма квадратов	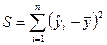Остаточная сумма квадратов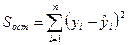

Аналогичные процедуры проведите и для второй выборки.

5. Вычислите наблюдаемое значение критерия достоверности .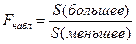

6. Найдите табличное значение критерия Фишера по уровню значимости 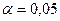и степеням свободы .

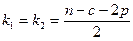6.1. Выделите клетку, в которой должно появиться значение 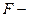критерия.

6.2. В главном меню выберите Вставка/функция.

6.3. В окне Категория выберите Статистические.

6.4. Затем в окне Функция выберите FРАСПОБР.

6.5. Заполните диалоговое окно.

6.6. Щелкните по кнопке ОК. Появится табличное значение критерия Фишера.

7. Сравните табличное значение критерия Фишера с наблюдаемым значением. Сделайте вывод.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Назовите пять предпосылок регрессионного анализа.

2. Проверка первых двух предпосылок регрессионного анализа.

3. В чем заключается суть гетероскедастичности? Причины появления гетероскедастичности.

4. Последствия гетероскедастичности.

5. Графический способ проверки гетероскедастичности

6. Тест Голдфельда – Квандта. Поясните в каком случае можно применять тест Голдфельда – Квандта?

Вариант №1

Страна	Ожидаемая продолжительность жизни при рождении в 1995 г., лет, Х	ВВП в паритетах покупательной способности, У
Никарагуа		7,4
Гана		7,4
Ангола		4,9
Пакистан		8,3
Мавритания		5,7
Зимбабве		7,5
Гондурас		7,0
Китай		10,8
Камерун		7,8
Конго		7,6
Шри-Ланка		12,1
Египет		14,2
Индонезия		14,1
Филиппины		10,6
Марокко		12,4
Папуа - Новая Гвинея		9,0
Гватемала		12,4
Эквадор		15,6
Доминиканская Республика		14,3
Ямайка		13,1
Алжир		19,6
Республика Эль-Сальвадор		9,7
Парагвай		13,5
Тунис		18,5
Белоруссия		15,6
Перу		14,0
Таиланд		28,0
Панама		22,2
Турция		20,7
Польша		20,0

Вариант №2

Страна	Индекс человеческого развития, У	Расходы домашних хозяйств, % к ВВП, Х
Австрия	0,904	56,1
Австралия	0,922	61,8
Англия	0,918	64,1
Белоруссия	0,763	59,1
Бельгия	0,923	63,3
Германия	0,906	57,0
Дания	0,905	50,7
Индия	0,545	57,1
Испания	0,894	62,0
Италия	0,900	61,8
Канада	0,932	58,6
Казахстан	0.740	71,7
Китай	0,701	48,0
Латвия	0,744	63,9
Нидерланды	0,921	59,1
Норвегия	0,927	47,5
Польша	0,802	65,3
Россия	0,747	53,2
США	0,927	67,9
Украина	0,721	61,7
Финляндия	0,913	52,9
Франция	0,918	59,9
Чехия	0,833	51,5
Швейцария	0,914	61,2
Швеция	0,923	53,1