2015-05-10
366
В первую очередь проверяется первая предпосылка МНК – проверяется случайный характер остатков. С этой целью строится график зависимости остатков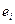 
от теоретических значений результативного признака 
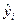. Если на графике нет направленности в расположении точек 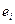, то остатки представляют собой случайные величины и МНК оправдан, теоретические значения 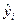хорошо аппроксимируют фактические значения 
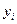. На графике рис. 1. получена горизонтальная полоса. Следовательно, 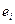– случайные величины.
Если 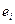зависят от 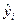, возможны следующие случаи:
1) остатки не случайны (рис. 2, 3. а);
2) остатки носят систематический характер (рис. 3 б). На данном рисунке отрицательные значения 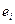соответствуют низким значениям 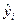, а положительные – высоким значениям;
3) остатки не имеют постоянной дисперсии (рис. 3 в).
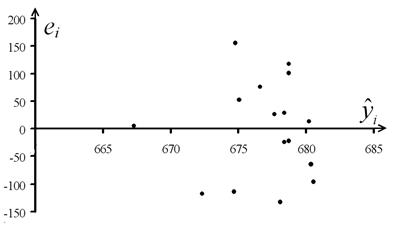
Рис. 1.
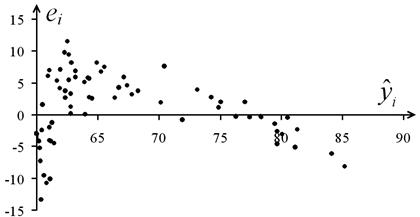
Рис. 2.
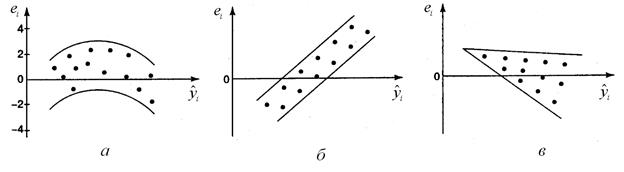
Рис. 3.
В данных случаях необходимо либо применять другую функцию, либо ввести дополнительную информацию и заново строить уравнение регрессии до тех пор, пока остатки не станут случайными величинами.
Вторая предпосылка (нулевая средняя величина остатков) означает, что:
1) 
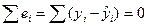для линейных моделей и моделей, нелинейных относительно включаемых переменных. 
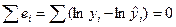для моделей нелинейным по оцениваемым параметрам и приводимых к линейному виду логарифмированием.
2) 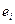не зависит от величины 
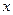. На рис. 4. графики остатков расположены в виде горизонтальной полосы, следовательно, 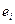не зависит от величины .
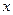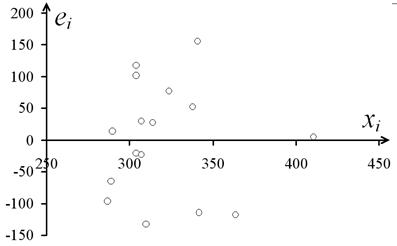
Рис. 4.
Если график показывает зависимость 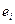от величины 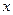, то модель не адекватна.
Причины:
1) нарушена 3–я предпосылка МНК;
2) неправильная спецификация модели и в нее требуется ввести дополнительные члены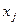 
, например, 
, или преобразовать значения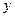 
.
Скопление точек в определенных участках значений фактора 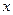говорит о наличии систематической погрешности модели. Корреляция 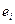с 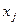позволяет проводить корректировку модели, в частности, использовать кусочно-линейные модели.
Совершенно необходимым для получения по МНК состоятельных оценок параметров регрессии является соблюдение 3–й и 4–й предпосылок.
