Метод понижения порядка производной

Решить дифференциальное уравнение – означает получить функцию y(t), меняющуюся во времени. Для составления структурной схемы решения применим метод понижения порядка производной, который сводится к пяти этапам.

Этап1. Разрешим дифференциальное уравнение (1) относительно высшей производной:

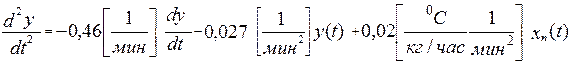(4)

Этап 2. Предположив, что в точке А 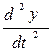известно в любой момент времени, с помощью интегрирующего звена и с учетом начальных условий получим в точке В значение 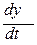. Затем, с помощью еще одного интегратора, в точке С получим значение искомой функции y(t).

Рис.2.

Этап 3. Посмотрите теперь на правую часть уравнения (4). Она представляет собой сумму трех функций времени, взятых с постоянными коэффициентами:

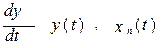
Допустим, рис.3, что нам известны функции y(t) в точке С₁ и 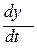в точке В₁. Теперь, просуммировав их с коэффициентами, соответствующими правой части (4) получим вторую производную 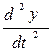. Таким образом, на выходе сумматора, в точке А₁, будет величина 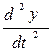, известная в любой момент времени.

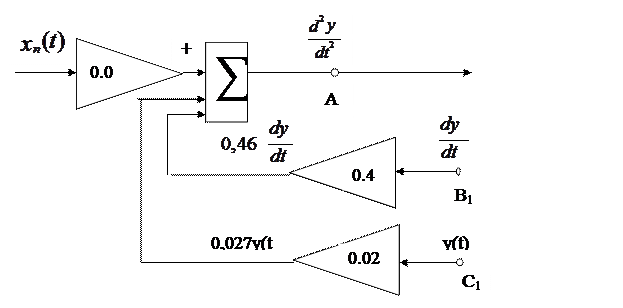
Рис.3

Этап.4. Равенство (4), которое происходит из физической сущности моделируемого объекта требует, чтобы оно (это равенство) выполнялось в любой момент времени t. Реализовать это требование легко – достаточно замкнуть схемы, показанные на рис.2 и рис.3. При этом сольются точки А и А₁, В и В₁, С и С₁. (рис.4).

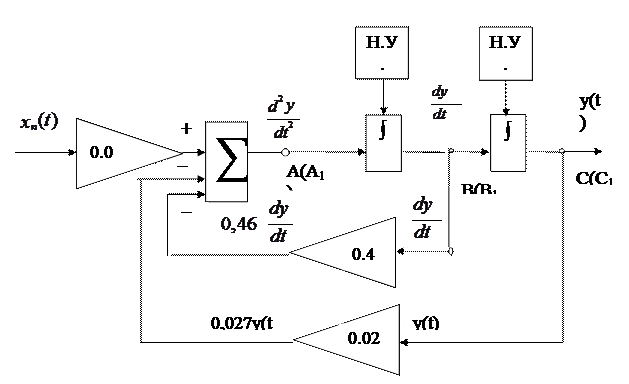
Рис.4.

Этап 5. Установить начальные условия, которые определяют единственность решения дифференциального уравнения.

Инструментарий SIMULINK пакета MatLab как раз и позволяет моделировать и исследовать поведение систем, описываемых любыми (линейными, линейными с переменными и нелинейными) дифференциальными уравнениями.

Единственное требование к дифференциальным уравнениям – они должны быть представимы в виде структурных схем, подобных указанной на рис.4.