Лабораторная работа №3. Исследование методов имитационного моделирования модулированных сигналов

3.1. Краткие теоретические сведения

При модуляции параметров немодулированного (несущего) колебания

u_ω= U₀cos(ω₀t+ φ), (3.1)

формируется модулированное колебание, которое в общем случае можно записать в виде

u= U(t)cos[ω₀t+ φ(t)] = U(t)cosΦ(t) (3.2)

где (ω₀ — несущая частота; Φ(t) = (ω₀t + φ(t) — мгновенная фаза колебания.

Амплитуда U(t) и фазовый сдвиг φ(t) колебания (3.2) изменяются в зависимости от модулирующего сигнала s(t).

Спектр модулированного колебания (3.2) обычно оказывается шире спектра модулирующего сигнала.

3.1.1. Амплитудно-модулированные колебания

При амплитудной модуляции происходит изменение амплитуды U(t) модулированного колебания при постоянной начальной фазе φ. Выражение (3.2) принимает вид

u_AM= U(t)cos(ω₀t+ φ). (3.3)

Огибающая (амплитуда) модулированного колебания изменяется вокруг среднего значения U₀ и связана с модулирующим сигналом s(t) линейным соотношением

U(t) = U₀+ k_As(t), (3.4)

где k_A — коэффициент пропорциональности, такой, что при любых t обеспечивается U(t) ³ 0.

Модуляция гармоническим сигналом (тональная модуляция). Если модулирующий сигнал s(t) является гармоническим колебанием, т. е.

s(t) = Scos(Ωt+ ψ), (3.5) то, согласно (3.4), огибающая модулированного колебания имеет вид

U(t) = U₀+ ΔUcos(Ωt+ ψ), (3.6)

где Ω — частота модуляции (Ω << ω₀); ψ — начальная фаза огибающей; ΔU = k_AS — наибольшее отклонение амплитуды от среднего значения. Мгновенное значение подобного тонально-модулированного колебания выражается как

u_AM= U₀[1 + Mcos(Ωt+ ψ)]cos(ω₀t+ φ) (3.7)

где отношение М = ΔU/U₀, называемое коэффициентом модуляции, является одним из основных параметров AM колебания.

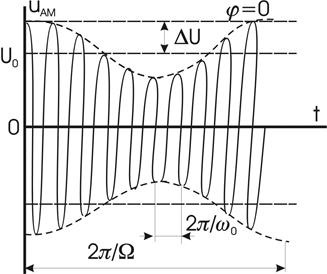
Рис. 3.2

Ha рис. 3.2 изображена временная диаграмма колебания (3.7).

колебание u_AM имеет дискретный спектр, состоящий из трех высокочастотных спектральных составляющих. Первое слагаемое в правой части представляет собой исходное немодулированное колебание с частотой ω₀ и начальной фазой φ. Второе и третье слагаемые называют соответственно верхней и нижней боковыми составляющими. Они расположены симметрично относительно несущего колебания на верхней (ω₀ + Ω) и нижней (ω₀ – Ω) боковых частотах модуляции и имеют соответственно начальной фазы (φ + ψ) и (φ — ψ). Амплитуды боковых составляющих равны U_oM/2. При неискаженной модуляции U₀M/2 £ U₀/2 (M £ 1). Рис. 3.3 иллюстрирует формирование спектра AM колебания. На рис. 3.3, a изображен спектр колебаний до модуляции. При модуляции (в результате перемножения функций cos Ωt - cos ω₀t) происходит сдвиг спектра модулирующего сигнала на величину ω₀ и расширение спектра (рис. 3.3, б). Ширина полосы частот 2Δω_AM, занимаемой АМ колебанием, определяется удвоенной частотой модулирующего сигнала

2Δω_AM = 2Ω

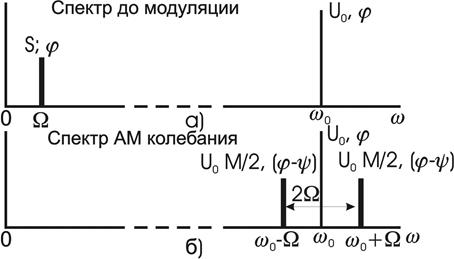
Рис. 3.3

Модуляция произвольным периодическим сигналом. Периодический модулирующий сигнал s_п(t) может быть представлен рядом Фурье вида (2.8):

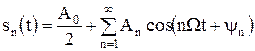(3.9)

где Ω — основная частота модулирующего сигнала.

Если отнести постоянную составляющую А₀/2 ряда Фурье к амплитуде несущего колебания U₀, то огибающую U(t) модулированного колебания можно записать так:

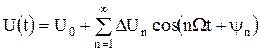(3.10)

где ΔU_n = k_AA_n.

Каждая спектральная составляющая модулирующего сигнала (3.9) так же, как при тональной модуляции, создает две боковые частоты в спектре модулированного колебания.

Если ширину спектра ΔΩ модулирующего сигнала определить как

ΔΩ= Ω_max = mΩ,

где Ω_max — максимальная частота, которая учитывается в спектре этого сигнала, соответствующая m-й гармонике, то ширина спектра AM колебания равна

2Δω_AM = 2Ω_max.

Модуляция непериодическим сигналом. В случае модуляции непериодическим сигналом s(t) со спектральной плотностью G(ω) огибающую U(t) и AM колебание u_АМ(t) можно записать в виде

U(t) = U₀ + k_As(t), (3.12)

u_AM(t) = [U₀ + k_As(t)]cos(ω₀t + φ) (3.13)

спектральная плотность огибающей, сосредоточенная в области нижних частот, «раздваивается» и переносится в область высоких частот, смещаясь на ±ω₀. спектральная плотность G_АM(ω) AM колебания имеет две составляющие: 1/2G_u(ω – ω₀) и 1/2G_u(ω + ω₀), сконцентрированные вблизи частот ω₀ и -ω₀ соответственно. Ширина спектра 2Δω_AM AМ колебания вдвое превышает ширину спектра Δω_U огибающей.

3.1.2. Колебания с угловой модуляцией

Общие понятия. При угловой модуляции под действием модулирующего сигнала происходит изменение фазового сдвига φ(t) несущего колебания (3.1) при постоянной амплитуде U₀. Модулированное колебание (3.2) принимает вид

u(t) = U₀cos[ω₀t+ φ] = U₀cosΦ(t) (3.23)

Изменение фазового сдвига φ(t) происходит как при модуляции мгновенной частоты ω(t), так и при модуляции непосредственна фазового сдвига ω(t) колебания (3.23). Поэтому различают два вида угловой модуляции: частотную модуляцию (ЧМ) и фазовую модуляцию (ФМ).

При частотной модуляции имеет место линейная связь между мгновенной частотой ω(t) колебания (3.23) и модулирующим сигналом s(t):

ω(t) = ω₀+ ω_дs(t)*, (3.25)

где ω_д — девиация частоты, т. е. максимальное отклонение частоты ω(t) от ω₀.

Полная фаза Φ(t) ЧМ колебания определяется как интеграл от мгновенной частоты (3.25)

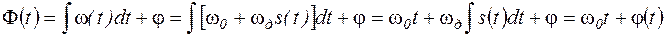(3.26)

где фазовый сдвиг

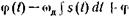(3.27)

При этом ЧМ колебание принимает вид

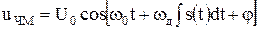(3.28)

Таким образом, фазовый сдвиг φ(t) ЧМ колебания изменяется по закону интеграла от модулирующего сигнала s(t).

Частотно-модулированный сигнал можно получить на выходе частотного модулятора, в котором модулирующий сигнал s(t) либо непосредственно управляет угловой частотой ω(t) несущего колебания в соответствии с выражением (3.25), либо после интегрирования управляет фазовым сдвигом φ(t) несущего колебания согласно выражению (3.27).

При фазовой модуляции в соответствии с модулирующим сигналом s(t) изменяется фазовый сдвиг

φ(t) = φ+ ms(t), (3.29)

где φ — начальная фаза немодулированного колебания; m — индекс угловой модуляции, т. е. максимальное отклонение фазы колебания (3.23) от начальной фазы φ. Учитывая (3.29), полную фазу Φ(t) модулированного колебания (3.23) можно определить по формуле

Φ(t) = ω₀t+ ms(t) + φ (3.30)

При этом фазомодулированное колебание принимает вид:

u_ФМ= U₀cos[ω₀t+ ms(t) + φ] (3,31)

Мгновенная частота ФМ колебания, равная

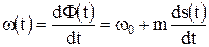(3.32)

изменяется по закону производной от модулирующего сигнала s(t).

Следовательно, ФМ сигнал можно получить на выходе фазового модулятора, в котором модулирующий сигнал s(t) либо непосредственно управляет фазовым сдвигом φ(t) несущего колебания согласно выражению (3.29), либо.после дифференцирования управляет угловой частотой ω(t) несущего колебания в соответствии с (3.32).

Ограничимся рассмотрением ЧМ и ФМ колебаний при модуляции гармоническим сигналом

s(t) = ScosΩt (3.33)

Сравним основные характеристики сигналов с частотной и фазовой модуляцией