Лабораторная работа №2. исследование дискретного спектра ФУРЬЕ электрокардиосигнала

2.1 Краткие теоретические сведения

Дискретное преобразование Фурье (ДПФ) широко применяется в цифровой технике для обработки сигналов. Прямое ДПФ выполняется над последовательностью дискретных комплексных величин 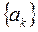конечной длительности. В результате получается также конечной длительности дискретная последовательность комплексных величин 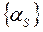, представляющих спектр указанной исходной последовательности. При обратном ДПФ по второй последовательности находится первая из них. Каждаяиз этих последовательностей содержит одинаковое количество N дискретных отсчетов.

Преобразование Фурье можно рассматривать как линейное преобразование с ядром

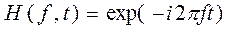. (2.1)

Если спектр сигнала а (t) лежит в интервале [-F, F],то такой сигнал согласно теореме Шеннона-Котельникова может быть восстановлен по своим дискретным отсчетам а (k/2F), согласно интерполяционной формуле

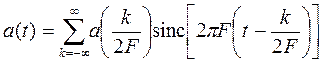, (2.2)

где k-номер отсчета, 1/(2F) – найквистовская частота дискретизации.

ПреобразованиеФурье сигнала (2.2) имеет вид

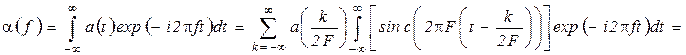
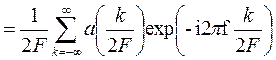. (2.3)

Рассмотрим периодический сигнал с периодом Т:

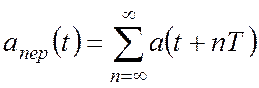. (2.4)

Пусть 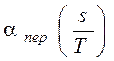- отсчеты спектра сигнала 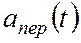, взятого на отрезке .

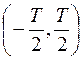Если Т достаточно велико, а сигнал 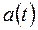достаточно быстро спадает до нуля на интервале Т, так что его искажениями в сумме (2.4) за счет наложения периодов можно пренебречь, то

,

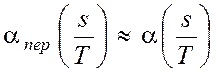отсюда

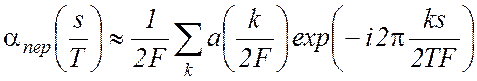, (2.5)

причем суммирование по k проводится в пределах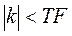

Значения T и F можно всегда выбрать так, чтобы величина 2TF была целой. Обозначим ее N. Обозначим также

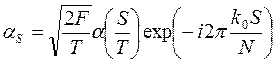, (2.6)

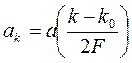. (2.7)

Здесьk ₀ выбрано так, чтобы суммирование в (2.5) могло производиться по k от 0 до N-1. Тогда, подставляя (2.7) в (2.5), а (2.5) в (2.6),получим

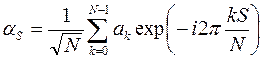. (2.8)

Это соотношение называется ДПФ.

ДПФ обратимо:

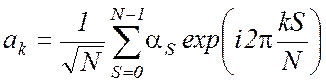. (2.9)

Ядро ДПФ – матрица

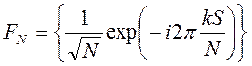(2.10)

является дискретным представлением непрерывного преобразования Фурье (k - номер столбца, S - номер строки).

Коэффициенты 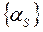ДПФ последовательности 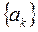приближенно равны отсчетам спектра сигнала 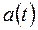, периодически продолженного с периодом Т, взятым с шагом 1/T. Такова связь ДПФ с непрерывным преобразованием Фурье. Из предположения ограниченной протяженности сигнала вытекает, что для его спектра справедлива теорема отсчетов и что, следовательно, он может быть восстановлен по величине 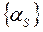– коэффициентам ДПФ отсчетов сигнала.

Вместо представлений ДПФ в виде сумм удобнее пользоваться матричными обозначениями. В этих обозначениях одномерное ДПФ можно записать так:

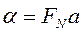(2.11)

где a — матрица-столбец, составленная из отсчетов преобразуемой последовательности ;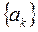

α – матрица-столбец, составленнаяиз коэффициентов ДПФ ;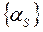

F_N - квадратная матрица ДПФ порядка N.

Матрица ДПФ относятся к классу так называемых унитарных матриц, для которых обратная матрица получаетсяих транспонированием и заменой элементов на комплексно-сопряженные.

Общая формула для элемента матрицы, расположенного в k-м столбце и в s-й строки, выглядит так

F(s,k)=exp(-i2π(s-1)(k-1)/N),

где 1≤s≤N, 1≤k≤N,

что соответствует формуле (2.10). Нормирование по N можно проводить после перемножения вектора а на столбец матрицы F, то есть нормирующий коэффициент может быть учтен в формуле (2.11), а не в (2.10).

2.2. Объект исследования

Объектом исследования в данной лабораторной работе являются дискретные отсчеты электрокардиосигналов, записанные в файлах, полученных в результате выполнения лабораторной работы №1.

2.3. Цель работы

Изучить методы получения дискретного спектра биомедицинских сигналов

2.4. Содержание работы и порядокее выполнения

1. Задавшись соответствующим базисом (по умолчанию базисом Фурье) запишите матрицу спектрального преобразования для этого базиса.

2. Зарисуйте схему алгоритма и создайте программный модуль для выбранного спектрального преобразования.

3. Подайте на вход созданного в п. 3 программного модуля сигнал, файл данных которого получен в результате выполнения лабораторной работы №1. Распечатайте сигнал на выходе программного модуля. Сравните полученный спектр с теоретической картиной спектра.

4. Получить обратное ДПФ найденного сигнала. Используя один из методов интерполяции постройте график найденной функции. Сравните полученный график с графиком исходного сигнала.

2.5 Содержание отчета

1. Распечатка графика исходного сигнала.

2. Распечатка графика ДПФ ( спектральной плотности).

4. Распечатка графика обратного ДПФ.

5. Схемы алгоритмов и листинги созданных программ

4. Электронная форма на дискете 3.5”.

5. Выводы.

2.6. Контрольныевопросы

1. Как изменятся формулы (2.10) и (2.11), если в качестве ядра преобразования в формуле (2.1) использовать 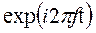? Как при этом изменится спектр ?

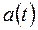2. Составьте матрицу-ядро обратного ДПФ.

3. Какова связь угловой частоты с круговой? Какие преимущества дает использование круговой частоты в формулах (2.10) и (2.11)?

4. Что произойдет, если мы увеличим размерность матрицы отсчетов? Уменьшим размер?

5. Почему при разложении действительных функций времени 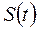можно использовать систему комплексных базисных функций ?

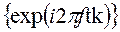6. При какихусловиях можно пользоваться формулой прямого ДПФ?

7. Что происходит со спектром при сжатии (растяжении) сигнала?

8. Как осуществляется дискретизация непрерывного сигнала по времени? Чем определить интервал дискретизации?

9. В каких случаях целесообразно использовать ДПФ, и для каких целей?

10. С чем связано требование ограниченности спектра сигнала, представляемого дискретным рядом Фурье? Что будет, если это требование не выполнено?

11. Что будет, если спектр сигнала оказался шире, чем предполагалось при представлении его дискретным рядом Фурье?

12. Коэффициенты разложения функций s(t) и f(t) по базису {exp(iωt)} равны, соответственно, {1, 0, 1, 2, 1} и {4, 0, 1}. Определите коэффициенты разложения произведения этих функций в том же базисе.

13. Как изменится преобразование Фурье 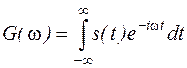при умножении s(t) на cosω₀t?

14. Чем отличается комплексный спектр Фурье от вещественного?

15. Как изменится преобразование Фурье 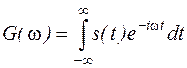при умножении s(t) на s(t-t_з), где t_з – некоторая константа?

16. Произвольная функция s(t) задана на интервале (0; 3π/2). Как запишется тригонометрический базис для этой функции?

17. Как изменится преобразование Фурье 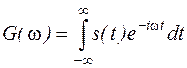, если аргумент t заменить на t-t_з, где t_з – некоторая константа?

18. Чем отличается спектр функции, полученный при ее разложении в комплексный ряд, от спектра функции, полученного при ее разложении в ряд по множеству Фурье?

19. Доказать, что энергетический спектр белого шума s(ω)=N₀/2.

20. Известно, что множество Фурье ортогонально на любом интервале, длина которого 2π. Как разложить функцию по этому базису на этом интервале, если ее период составляет ?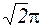

21. Произвольная функция s(t) задана на интервале (-1,1). Как запишется тригонометрический базис для этой функции?

22. Известно, что множество Фурье ортогонально на любом интервале, длина которого 2π. Как разложить функцию по этому базису на этом интервале, если ее период составляет (6/2,2)π?

23. Почему для разложения действительной функции s(t) можно использовать систему комплексных базисных функций ?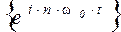

24. Пусть мы раскладываем в ряд Фурье функцию вида

.

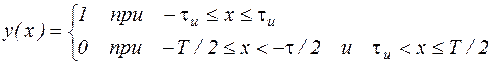Как изменится спектр этой функции при уменьшении τ_и?

25. Пусть мы определяем преобразование Фурье функции вида

.

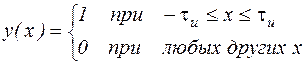Как изменится спектр этой функции при увеличении τ_и?

2.7. Порядок защиты работы

Работа может быть зачтена, если студент представил отчет согласно п.2.5, исследуемые в работе сигналы соответствуют индивидуальному варианту, электронная форма соответствует представленному тексту, и студент дал исчерпывающие ответы на 10 произвольных вопросов из п.2.6.

Литература

1. Марпл.-мл. С.Л. Цифровой спектральный анализ и его приложения: Пер. с англ.- М.: Мир, 1990.- 584 с.

2. Методические указания к курсу лабораторных работ «Исследование линейных дискретных преобразований» /Курск. гос. техн. ун-т; Сост. С.А. Филист, Курск. КПИ.1993. 13 с.