Көп өлшемдi теңдеулердiң жағдайына Кранко-Никольсон схемасының жалпылауын жергiлiктi - бiр өлшемдi операторларымен қарап шығамыз.
Сонымен қатар бұрынғыдай 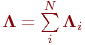 . Егер әрбір оператордың коэффициенті уақытқа тәуелді болса, олар белгілі бір уақыт аралығында алынады
. Егер әрбір оператордың коэффициенті уақытқа тәуелді болса, олар белгілі бір уақыт аралығында алынады 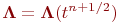 . Қарапайым мазмұны үшін екі жағдайды қарастырамыз.
. Қарапайым мазмұны үшін екі жағдайды қарастырамыз.
Ыдырау схемасын мына бағыт бойынша қарастырамыз:
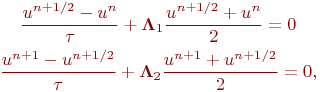
Уақыт бойынша операторлық шешімі келесі түрде жазылады 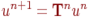 .
.
Ауыспалы оператор үшін мына формула алынады:
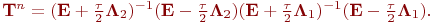
Орындалу кезінде мына шарт 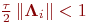 тұрақты, уақыт бойынша екінші ретпен аппроксимацияланады, егер оператор
тұрақты, уақыт бойынша екінші ретпен аппроксимацияланады, егер оператор 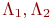 коммутативті және біріншісі жоқ болса.
коммутативті және біріншісі жоқ болса.
8.2.3. Ыдырау әдісінің жалпы құрылымы.
Жергілікті - бір өлшемді дифференциалдық 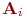 операторының әр қадамын уақыт бойынша
операторының әр қадамын уақыт бойынша 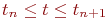 ауыстырамыз. Ыдырау схемасын келесі жалпы түрде қарастырамыз:
ауыстырамыз. Ыдырау схемасын келесі жалпы түрде қарастырамыз:
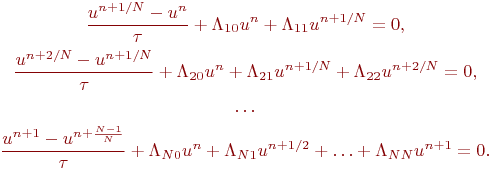
Шарт тұрақтылығы ыдырау схемасында былай көрінеді:
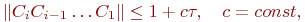 онда
онда 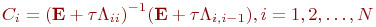
Екі сатылы ыдырау схемасы коэффициенттерімен келесі түрде беріледі:
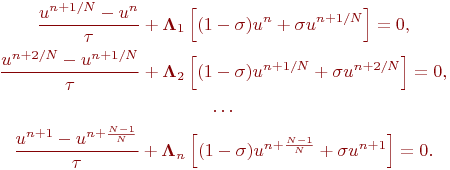
Егер бұл ыдырау схемасында жоғарғы және төменгі қабаттарды уақыт бойынша теңестірсек 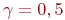 , онда басқарушы
, онда басқарушы 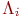 операторы екінші ретпен уақыт бойынша аппроксимацияланады.Егер әрбір оператор
операторы екінші ретпен уақыт бойынша аппроксимацияланады.Егер әрбір оператор 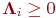 болса, онда бұл схема тұрақты болады.
болса, онда бұл схема тұрақты болады.
8.2.4. Жылулық теңдігіне байланысты ыдырау схемасы
Стационар емес жылулық теңдігін қарастырамыз
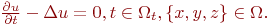
Бұл жерде Лаплас операторы 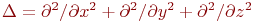 анықталған. Оны суммалық үш жергілікті – бір өлшемді оператор
анықталған. Оны суммалық үш жергілікті – бір өлшемді оператор 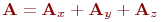 ретінде жазуға болады. Сәйкесінше бұл оператор
ретінде жазуға болады. Сәйкесінше бұл оператор 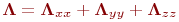 тең болады, онда
тең болады, онда 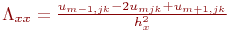 екінші оператор
екінші оператор 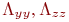 соңғы және әр түрлі бағытты есептеуде толығымен анықталады. Жергілікті – бір өлшемді оператор жылулық теңдігі үшін мына теңдікке тең болады.
соңғы және әр түрлі бағытты есептеуде толығымен анықталады. Жергілікті – бір өлшемді оператор жылулық теңдігі үшін мына теңдікке тең болады.
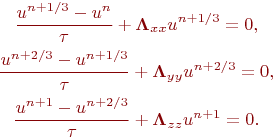
Аппроксимация ретін көтеру үшін өлшем бойынша схеманы қолдануға болады.
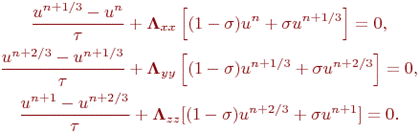
8.3. Компоненттік екі циклды ыдырау әдісі
Бұл әдіс үшін 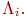 коммутативті операторының талабы қойылмайды. Уақыт бойынша бір қадам аралығында емес сандық шешімін қарастырамыз (8.1), [tn, tn+1] бөлігінде, ал екі қадам үшін [tn-1, tn+1]. Енді жергілікті – бір өлшемді оператор уақыттан тәуелді болсын, онда олар
коммутативті операторының талабы қойылмайды. Уақыт бойынша бір қадам аралығында емес сандық шешімін қарастырамыз (8.1), [tn, tn+1] бөлігінде, ал екі қадам үшін [tn-1, tn+1]. Енді жергілікті – бір өлшемді оператор уақыттан тәуелді болсын, онда олар 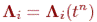 бөлігінің ортасында анықталады.Ыдырау схемасын жазамыз:
бөлігінің ортасында анықталады.Ыдырау схемасын жазамыз:
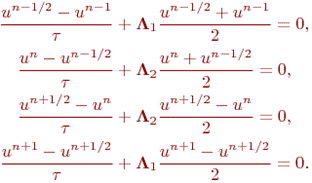
| (8.6) |
Ескертпе көрсетілген бұл әдіс операторлық түрде былай жазылады 
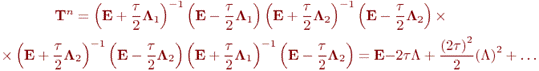
Егер жергілікті – бір өлшемді оператор шартты 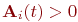 болса, онда оның шешімі және
болса, онда оның шешімі және 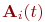 матрица элементі (8.6) схемасында шартты түрде, (8.1) схемасында екінші ретпен аппроксимацияланады.
матрица элементі (8.6) схемасында шартты түрде, (8.1) схемасында екінші ретпен аппроксимацияланады.
Бірінші ретті емес дифференциалдық теңсіздік үшін
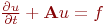
Ыдырау әдісі әр түрлі аппроксимация түрінде берілуі мүмкін
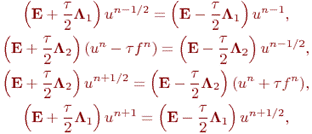 онда fn = f(tn).
онда fn = f(tn).
Операторлық түрдегі шешім 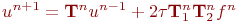
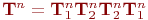
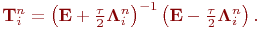
Бірінші ретті емес дифференциалдық теңсіздік үшін 
 сәйкесінше әр түрлі аппроксимациянын қолданамыз:
сәйкесінше әр түрлі аппроксимациянын қолданамыз:
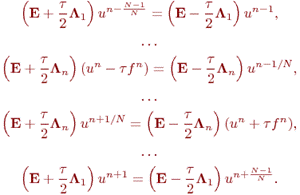
Екі циклды ыдырау әдісі үшін математика – физика есептерінің қолданылу мысалдарын қарастырамыз.
 2015-05-12
2015-05-12 657
657








