Пример 1. Решите систему по правилу Крамера, сделайте проверку.
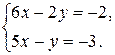
Решение.
Шаг 1. Вычисляем определитель D, составленный из коэффициентов при неизвестных.
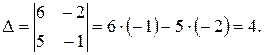
Этот определитель не равен нулю, значит, правило Крамера применимо и система имеет единственное решение.
Шаг 2. Вычисляем определитель 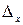 . Этот определитель получается из D заменой первого столбца столбцом свободных членов, т.е. правых частей уравнений.
. Этот определитель получается из D заменой первого столбца столбцом свободных членов, т.е. правых частей уравнений.
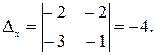
Теперь можно вычислить значение х: 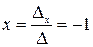 .
.
Шаг 3. Вычисляем определитель 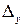 . Этот определитель получается из D заменой второго столбца столбцом правых частей уравнений.
. Этот определитель получается из D заменой второго столбца столбцом правых частей уравнений.
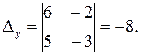
Вычисляем значение y: 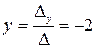 .
.
Шаг 4. Сделаем проверка. Подставим найденные значения х и у в уравнения системы.
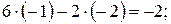
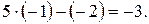
Видим, что оба равенства верные, значит найденное решение верное.
Ответ: 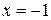 ,
, 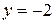 .
.
 2015-05-10
2015-05-10 362
362








