Пример 1. Решите систему уравнений
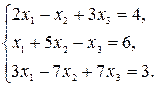
Решение.
Шаг 1. Запишем матрицу этой системы
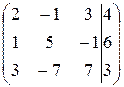 .
.
Шаг 2. Приведем эту матрицу к ступенчатому виду. Сначала поменяем первую и вторую строки местами
 .
.
Получим нули в первом столбце во второй и третьей строках. Для этого вычитаем из второй строки первую, умноженную на 2, а из третьей строки вычитаем первую, умноженную на 3. Эти преобразования записаны справа от матрицы. Получаем
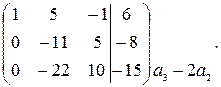
Получим нуль во втором столбце в третьей строке. Для этого выполним указанное преобразование. Получаем
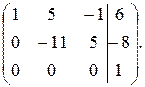
Шаг 3. Получилась строка, в которой до черты стоят нули, а после черты ненулевое число (третья строка). Делаем вывод: система не имеет решений.
Ответ: система не имеет решений.
Пример 2. Решите систему уравнений
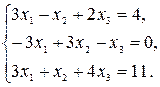
Решение.
Шаг 1. Запишем матрицу этой системы
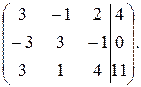
Шаг 2. Приведем эту матрицу к ступенчатому виду
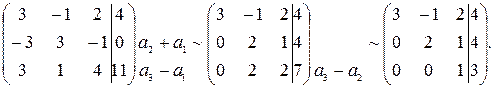
Шаг 3. Число строк в ступенчатой матрице совпадает с числом неизвестных, значит, решение единственное.
Шаг 4. Найдем решение. Для этого выполним преобразования.

Из последней матрицы получаем ответ 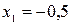 ,
, 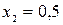 ,
, 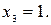 Этот ответ можно также записать в виде тройки чисел
Этот ответ можно также записать в виде тройки чисел 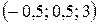 .
.
Ответ: 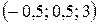 .
.
Пример 3. Решите систему уравнений
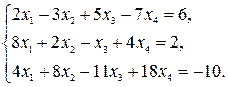
Решение.
Шаг 1. Запишем матрицу системы
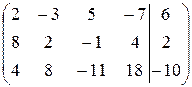 .
.
Шаг 2. Приведем матрицу к ступенчатому виду
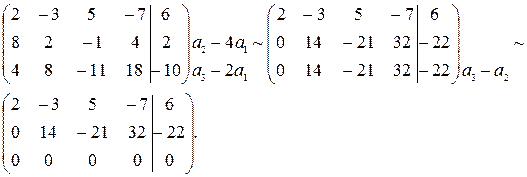
После вычеркивания нулевой строки получаем ступенчатую матрицу.
Шаг 3. В ступенчатой матрице число строк (2) меньше числа неизвестных (4). Делаем вывод: система имеет бесконечное множество решений.
Шаг 4. Выбираем основные и свободные неизвестные. Число основных неизвестных совпадает с числом строк в ступенчатой матрице (2). В качестве основных можно выбрать неизвестные, с которых начинаются уравнения. В данном случае 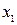 и
и 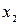 .
.
Шаг 5. Выразим основные неизвестные через свободные (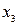 и
и 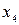 ). Выполним преобразования
). Выполним преобразования
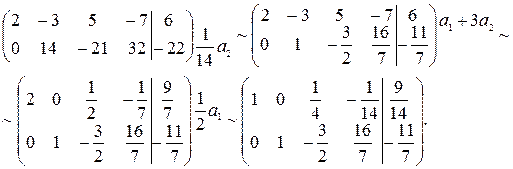
Возвращаемся к уравнениям: 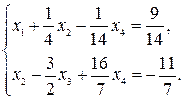
Выражаем из этих равенств основные неизвестные 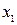 и
и 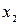 и записываем ответ.
и записываем ответ.
Ответ: 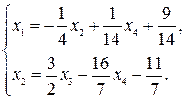
 2015-05-10
2015-05-10 415
415








