Пример 1. Найдите производную функции 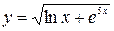 .
.
Решение.
Находим производную заданной функции, применяя правила дифференцирования сложной функции, суммы и вынесения числового множителя за знак производной.
Шаг 1. Это сложная функция поэтому вначале находим производную от 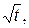 где
где 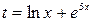 :
: 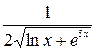 .
.
Шаг 2. Далее находим производную от подкоренной функции, которая представляет собой сумму двух слагаемых, при этом учитывая, что второе слагаемое также сложная функция: 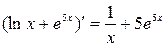 .
.
Шаг 3. Перемножаем полученные выражения и преобразовываем.
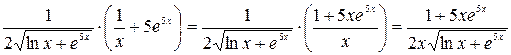 .
.
Итак, запись решения может выглядеть следующим образом:
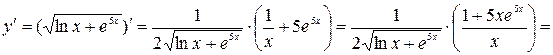
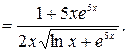
Ответ: 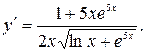
 2015-05-10
2015-05-10 571
571








