2015-05-10
975
Монотонной называется возрастающая или убывающая функция.
Теорема 1 (достаточное условие монотонности). Если функция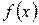 
дифференцируема на промежутке 
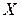и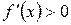 
(
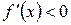) для всех 
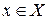, то 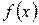возрастает (убывает) на промежутке .
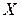Точка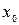 
называется точкой максимума (минимума) функции 
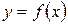, если существует такая 
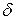-окрестность точки 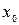, что для всех 
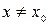из этой окрестности выполняется неравенство 
(
).
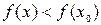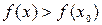Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции.
Т еорема 2 (необходимое условие экстремума). Если дифференцируема функция 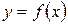имеет экстремум в точке 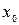, то ее производная в этой точке равна нулю 
.
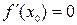Точки, в которых производная дифференцируемой функции равна нулю, называются стационарными точками.
Точки, в которых производная дифференцируемой функции равна нулю или не существует, называются критическими точками.
Теорема 3 (достаточное условие экстремума). Если непрерывная функция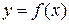 
дифференцируема в некоторой 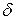-окрестности критической точки 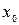и при переходе через нее (слева направо) производная 
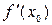меняет знак с плюса на минус, то 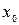– точка максимума функции; а если с минуса на плюс, то 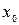– точка минимума.
Если в некоторой проколотой окрестности точки 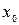производная 
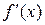имеет постоянный знак, то 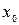не является точкой экстремума.
