2015-05-10
359
Пример 1. Исследовать функцию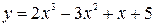 
и построить её график.
Решение.
Шаг 1. Найдем область определения функции. Данная функция определена для всех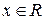 
, т.е.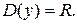 
Шаг 2.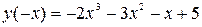 
, 
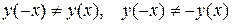, следовательно, функция ни четная, ни нечетная.
Шаг 3. Пересечение с осью Оy: подставим значение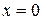 
в функцию. 
. 
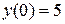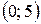– точка пересечения с осью Оy.
Пересечение с осью Ох. Решим уравнение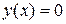 
,
, 
. 
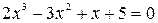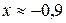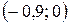– точка пересечения с осью Ох.
Шаг 4. Найдем производную функции:
.
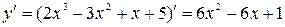Найдем критические точки. Решим уравнение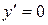 
.
,
, 
, 
, 
.
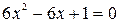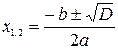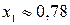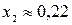Выясним знак производной функции в интервалах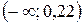 
, 
, 
.
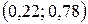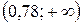| Промежуток |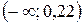
|
|
|
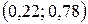
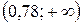
Знак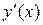 
| + | – | + |
| Монотонность | 
| 
| 
|
, 
; 
, 
.
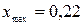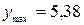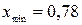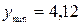Шаг 5. Найдем вторую производную функции
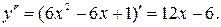
Решим уравнение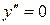 
. 
, 
.
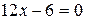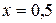Выясним знак второй производной функции в интервалах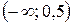 
, 
.
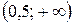| Промежуток |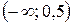
| 
|
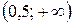
Знак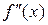 
| – | + |
| Направление выпуклости | Ç | È |
Так как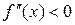 
на промежутке 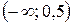, то функция выпукла на этом промежутке. На промежутке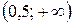 
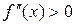, следовательно, функция вогнута на 
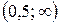. Так как при переходе через точку 
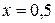вторая производная изменяет свой знак, то 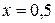– точка перегиба. 
.
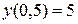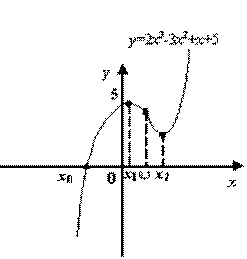
Шаг 6. Построим график функции:
