Метод замены переменной заключается во введении новой переменной интегрирования, т. е. подстановки. При этом заданный интеграл сводится к интегралу, который является табличным или к нему приводящимся.
Теорема 1. Пусть функция 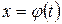 определена и дифференцируема на некотором промежутке
определена и дифференцируема на некотором промежутке 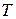 и пусть
и пусть 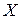 – множество значений этой функции, на котором определена функция
– множество значений этой функции, на котором определена функция 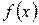 . Тогда, если на множестве
. Тогда, если на множестве 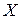 функция
функция 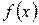 имеет первообразную, то на множестве
имеет первообразную, то на множестве 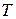 справедлива формула
справедлива формула
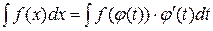 . (1)
. (1)
Формула (1) – формула замены переменной в неопределённом интеграле.
Теорема 2. Пусть функции 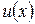 и
и 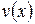 определены и дифференцируемы на некотором промежутке
определены и дифференцируемы на некотором промежутке 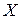 и пусть функция
и пусть функция 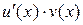 имеет первообразную на этом промежутке. Тогда на промежутке
имеет первообразную на этом промежутке. Тогда на промежутке 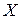 функция
функция 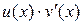 также имеет первообразную и справедлива формула
также имеет первообразную и справедлива формула
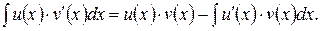 (2)
(2)
Формула (2) – формула интегрирования по частям в неопределённом интеграле.
Т.к. 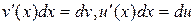 , то формулу (2) можно переписать в виде
, то формулу (2) можно переписать в виде
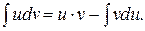 (2')
(2')
Применять формулу (2) следует, когда интеграл в правой части более прост для нахождения, нежели исходный. Рассмотрим два класса функций 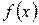 , которые целесообразно интегрировать по частям, и укажем, что в этих случаях при представлении подынтегрального выражения
, которые целесообразно интегрировать по частям, и укажем, что в этих случаях при представлении подынтегрального выражения 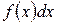 в виде произведения
в виде произведения 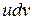 следует принять за
следует принять за 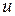 , а что за
, а что за 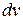 . Ниже через
. Ниже через 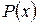 обозначен многочлен.
обозначен многочлен.
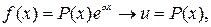
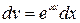 .
.
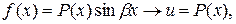
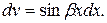
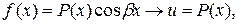
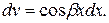
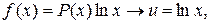
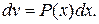
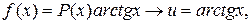
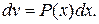
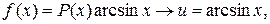
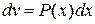 .
.
 2015-05-10
2015-05-10 259
259








