Задание 1. Составить уравнение плоскости, проходящей через точку А (2, 1, -3) и перпендикулярной вектору 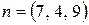 .
.
Решение:
По формуле (1) получаем уравнение искомой плоскости
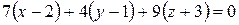 или
или 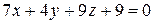 .
.
Задание 2. Составить уравнение плоскости, проходящей через точку А (2, 1, -3) и параллельной плоскости 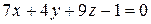 .
.
Решение:
Плоскость, параллельна плоскости 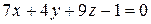 , очевидно перпендикулярна вектору
, очевидно перпендикулярна вектору 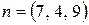 . Уравнение такой плоскости, проходящей через точку А (2, 1, -3) получено в задание №1.
. Уравнение такой плоскости, проходящей через точку А (2, 1, -3) получено в задание №1.
Задание 3. Составить уравнение плоскости, проходящей через три точки 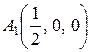 ,
, 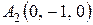 ,
, 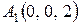 .
.
Решение:
Шаг 1. Составить уравнение плоскости (1), проходящей через точку 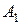 :
:
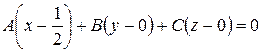
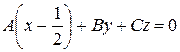 (*)
(*)
Шаг 2. Т.к. точки 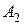 и
и 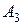 также лежат на этой плоскости, их координаты удовлетворяют уравнению плоскости, т.е.
также лежат на этой плоскости, их координаты удовлетворяют уравнению плоскости, т.е.
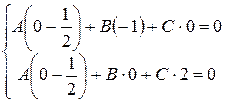 или
или 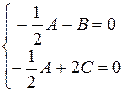 .
.
Выразим в системе уравнений две неизвестные через третью:
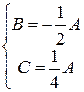 .
.
Шаг 3. Подставим полученные значения для В и С в уравнение плоскости (*):
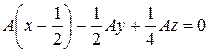 .
.
Откуда после сокращения на А получим общее уравнение плоскости:
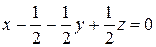 или
или 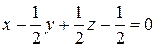 или
или 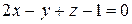 .
.
Задание 4. Составить уравнение прямой, проходящей через точку 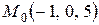 и:
и:
а) параллельной оси Оу;
б) точку 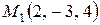 ;
;
в) параллельно прямой 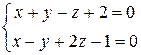 .
.
Решение:
а) Пусть точка 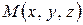 - произвольная точке, лежащей на искомой прямой, тогда вектор
- произвольная точке, лежащей на искомой прямой, тогда вектор 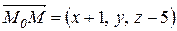 и единичный вектор
и единичный вектор 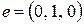 , направленный по оси Оу, лежат на параллельных прямых и имеет пропорциональные компоненты:
, направленный по оси Оу, лежат на параллельных прямых и имеет пропорциональные компоненты:
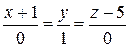 .
.
Получили искомое уравнение прямой.
б) Искомое уравнение прямой получим по формуле (6):
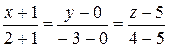 или
или 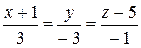
в) Шаг 1. Приведем уравнение прямой, заданной системой, к каноническому виду:
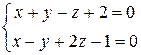 ,
, 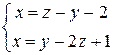
Приравняем выражение для х:
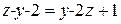 ,
, 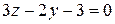 ,
,
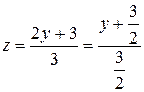 . (*)
. (*)
Сложим уравнения системы: 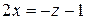 , откуда
, откуда
 . (**)
. (**)
Приравним (*) и (**), получим уравнение прямой:
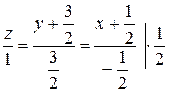
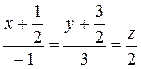
Шаг 2. Т.к. искомая прямая параллельна данной, то направляющий вектор у них может быть один 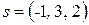 . Тогда по формуле (7) уравнение искомой прямой имеет вид
. Тогда по формуле (7) уравнение искомой прямой имеет вид
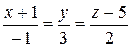 .
.
 2015-05-10
2015-05-10 1427
1427
