Вычислить следующие пределы:
4. 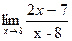
| 5. 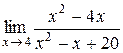
|
6. 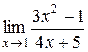
| 7. 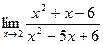
|
8. 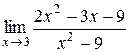
| 9. 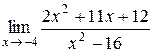
|
10. 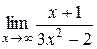
| 11. 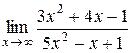
|
12. 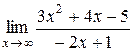
| 13. 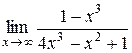
|
14. 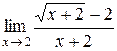
| 15. 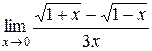
|
16. 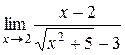
| 17. 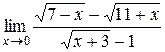
|
Ответы: 4) ∞; 5) 0; 6) 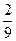 ; 7) -5; 8) 1,5; 9)
; 7) -5; 8) 1,5; 9) 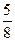 ; 10) 0; 11)
; 10) 0; 11) 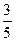 ; 12) ∞; 13)
; 12) ∞; 13) 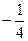 ; 14) 0; 15)
; 14) 0; 15) 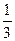 ; 16) 1,5; 17)
; 16) 1,5; 17) 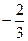 .
.
Домашнее задание.
18. 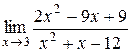
| 19. 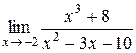
|
20. 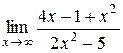
| 21. 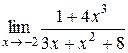
|
22. 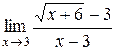
| 23. 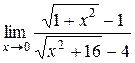
|
Ответы: 18) 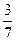 ; 19)
; 19) 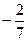 ; 20)
; 20) 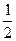 ; 21)
; 21) 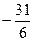 ; 22)
; 22) 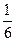 ; 23) 4.
; 23) 4.
Вычисление производных.
Краткие теоретические сведения.
Пусть функция 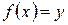 определена в окрестности точки
определена в окрестности точки 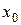 и точка
и точка 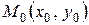 принадлежит графику функции.
принадлежит графику функции. 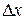 - приращение аргумента
- приращение аргумента 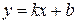
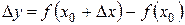 - соответствующее приращение функции
- соответствующее приращение функции  .
.
|
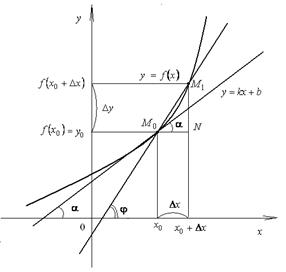
Угол наклона секущей, проходящей через точки 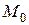 и
и 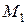 , равен
, равен 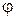 .
.
Угол наклона касательной к графику  т.
т. 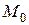 , равен
, равен 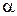 .
.
Из 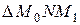 , находим
, находим 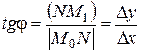 .
.
При 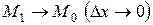 угол
угол 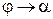 , а
, а 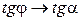 .
.
Т.о. 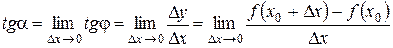 (1)
(1)
Производной функции  в точке
в точке 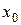 называют предел (1), если он существует и равен числу. Обозначение производной:
называют предел (1), если он существует и равен числу. Обозначение производной:
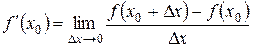 (2)
(2)
Из (1) и (2) следует, что угловой коэффициент касательной к графику  в точке
в точке 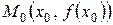 равен производной функции
равен производной функции 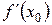 :
:
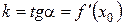 (3)
(3)
Основные правила нахождения производных
1) 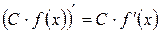 ;
;
2) 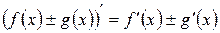 ;
;
3) 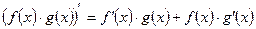 ;
;
4) 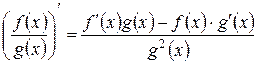 ;
;
5) 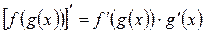 .
.
Таблица производных
1) 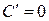
| 2) 
|
3) 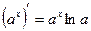 , , 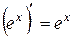
| 4) 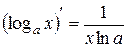 , , 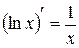
|
5) 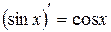
| 6) 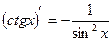
|
7) 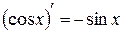
| 8) 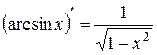
|
9) 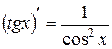
| 10) 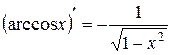
|
11) 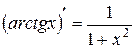
| 12) 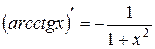
|
 2015-05-10
2015-05-10 291
291








