Рассмотрим последовательность 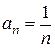 , где n =1, 2, 3, …:
, где n =1, 2, 3, …:

|
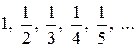
Видим, что все члены последовательности 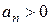 , но чем больше номер n, тем ближе
, но чем больше номер n, тем ближе 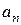 расположен к нулю. Этот факт записывают следующим образом:
расположен к нулю. Этот факт записывают следующим образом:
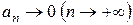 ;
; 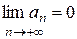 ;
; 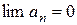 .
.
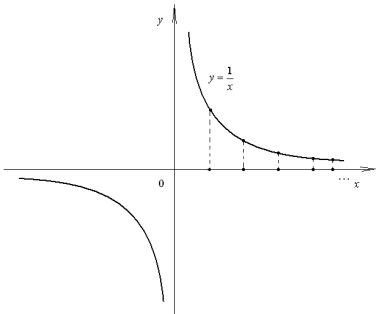 И говорят, что предел последовательности
И говорят, что предел последовательности 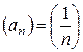 равен 0.
равен 0.
Аналогично можно найти пределы функции 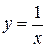 :
:
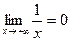 или
или 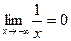 .
.
Говорят, что «предел функции 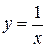 при x, стремящемся к
при x, стремящемся к 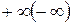 равен 0».
равен 0».
Рассмотрим несколько примеров пределов функций:
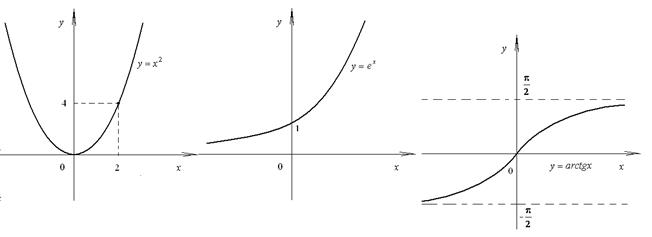
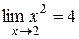 , , 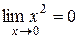
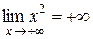
| 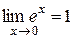 , , 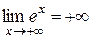
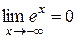
| 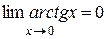
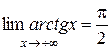
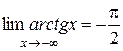
|
Предел функции может и не существовать. Например:
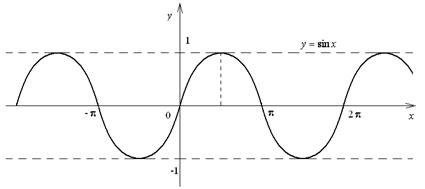
| 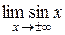 не существует, т.к. при не существует, т.к. при 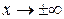 значение функции значение функции 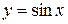 не стремятся к какому-нибудь определенному значению, а периодически меняются от -1 до 1. не стремятся к какому-нибудь определенному значению, а периодически меняются от -1 до 1.
|

| 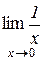 не существует, т.к. если х стремится к 0 слева, то значение функции стремится к не существует, т.к. если х стремится к 0 слева, то значение функции стремится к 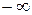 , а справа – к , а справа – к 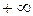 Единого значения предела при
Единого значения предела при 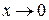 нет. нет.
|
При вычислении пределов часто возникают выражения:
- определенные 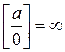 ,
, 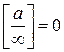 .
.
- неопределенные 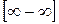 ,
, 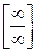 ,
, 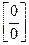 ,
, 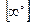 ,
, 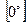 ,
, 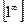 .
.
Алгоритм нахождения пределов функций 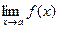 :
:
Шаг 1. Подставить значение  в формулу задания
в формулу задания  .
.
Если получится вполне определенный результат, то это и есть значение предела  при
при 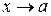 . Если же возникает неопределенность, то перейти к следующему шагу.
. Если же возникает неопределенность, то перейти к следующему шагу.
Шаг 2. Раскрыть неопределенность с помощью тождественных преобразований выражения  . Так, если в числителе и знаменателе находятся многочлены и возникает неопределенность вида
. Так, если в числителе и знаменателе находятся многочлены и возникает неопределенность вида 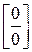 , то следует разложить числитель и знаменатель дроби на множители и сократить на множитель
, то следует разложить числитель и знаменатель дроби на множители и сократить на множитель 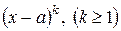 .
.
Если в числителе и знаменателе находятся многочлены и возникает неопределенность 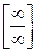 , то следует разделить числитель и знаменатель на х с наибольшим показателем степени числителя и знаменателя.
, то следует разделить числитель и знаменатель на х с наибольшим показателем степени числителя и знаменателя.
Шаг 3. Вновь подставить  в преобразование выражение
в преобразование выражение  и определить значение предела
и определить значение предела 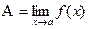 .
.
 2015-05-10
2015-05-10 324
324








