Решение типовых заданий

Задание 1. Найти :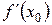

а) ;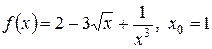

б) ;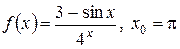

в) , .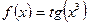

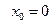Решение:

а) Шаг 1. Применим к производной 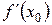правила дифференцирования 2) и 1):

.

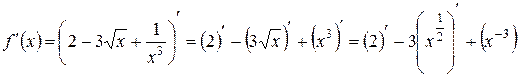Шаг 2. С помощью таблицы производных находим:

.

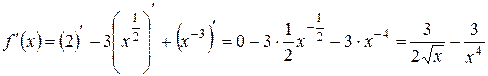Шаг 3. Найдем значение производной 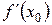в точке : .

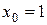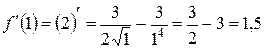б) Шаг 1. Применим к производной 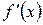4)-е правило дифференцирования:

.

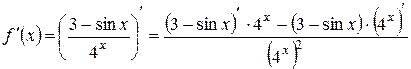Шаг 2. Применим 2)-е правило дифференцирования и таблицу производных находим:

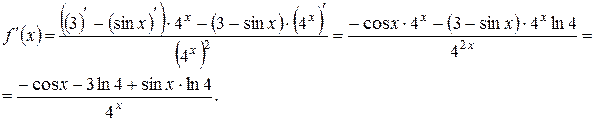
Шаг 3. Найдем значение 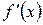в точке :

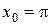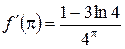
в) Шаг 1. Применим к 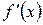5)-е правило дифференцирования сложной функции:

.

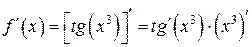Шаг 2. По таблице производных находим: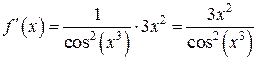

Шаг 3. Найдем значение 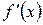в точке : .

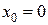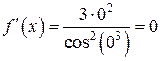Задание 2. Найти уравнение касательной к графику функции 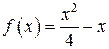в точке 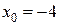. Сделать чертеж.

Решение:

Шаг 1. Найти значение производной функции 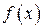в точке :

.

.

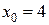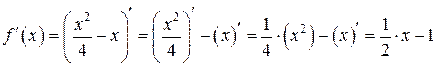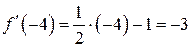Шаг 2. По формуле (3) найти угловой коэффициент касательной к графику 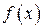в точке .

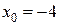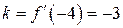
И общий вид уравнения касательной .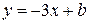

Шаг 3. Найти ординату точки касания :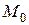

.

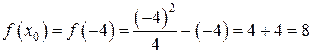Т.к. касательная проходит через точку 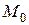, то можно подставить т. 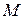в общее уравнение касательной и найти значение b:

отсюда b= -4.

Шаг 4. составить искомое уравнение касательной:

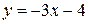или .

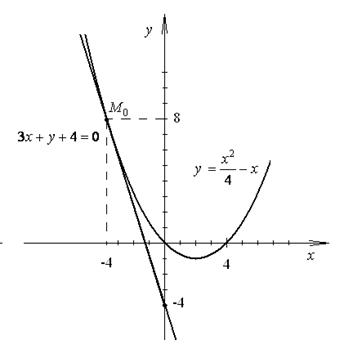
Шаг 5. Сделать чертеж