2015-05-10
216
Если функция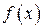 
имеет экстремум в точке 
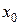, то либо 
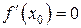(точку 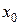называют стационарной) либо 
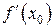не существует (точку 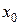называют критической).
Обратное утверждение неверно: критические и стационарные токи не обязательно являются точками экстремума.
Достаточное условие существования экстремума.
Если при переходе через точку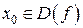 
производная функции 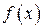меняет свой знак с плюса на минус, то точка 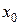есть точка максимума функции 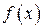, а если с минуса на плюс, то – точка минимума.
Алгоритм исследования функции 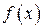на монотонность и экстремум
Шаг 1. Найти область определения функции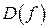 
.
Шаг 2. Найти производную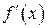 
.
Шаг 3. Найти стационарные и критические точки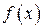
Шаг 4. Разбить 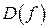на интервалы стационарными и критическими точками.
Шаг 5. Определить знак производной 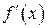в каждом из полученных интервалов и сделать выводы о промежутках монотонности и точках экстремума .
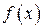Шаг 6. Вычислить экстремумы (экстремальные значения функции).
