Задание 1. Найти наибольшее и наименьшее значения функции 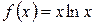 на
на 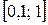 .
.
Решение:
Шаг 1. 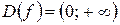 .
.
Шаг 2. 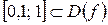 .
.
Шаг 3. 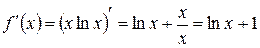 .
.
Шаг 4. Найдем стационарные точки  :
:
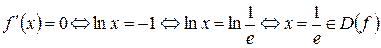 .
.
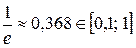 .
.
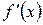 существует всюду в
существует всюду в 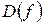 , поэтому критических точек
, поэтому критических точек  нет.
нет.
Шаг 5. 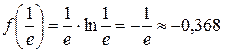 .
.
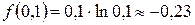
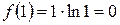 .
.
Шаг 6. 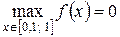 - наибольшее значение
- наибольшее значение  на
на 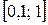 ;
;
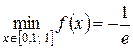 наименьшее значение
наименьшее значение  на
на 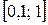 .
.
Задание для самостоятельного решения.
Задание 2. найти наибольшее и наименьшее значения функции  на указанном отрезке.
на указанном отрезке.
1) 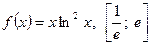 ; 2)
; 2) 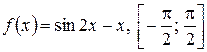 ; 3)
; 3) 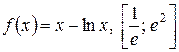 ;
;
4) 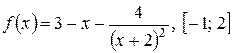 ; 5)
; 5) 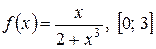 ; 6)
; 6) 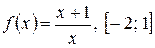 ;
;
7) 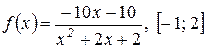 ; 8)
; 8) 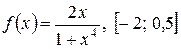 .
.
Ответы: 2.1) 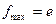 ,
, 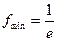 ; 2.2)
; 2.2) 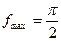 ,
, 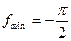 ; 2.3)
; 2.3) 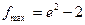 ,
, 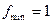 ; 2.4)
; 2.4) 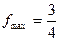 ,
, 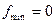 ; 2.5)
; 2.5) 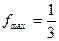 ,
, 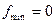 ; 2.6) нету; 2.7)
; 2.6) нету; 2.7) 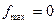 ,
, 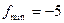 ; 2.8)
; 2.8) 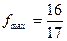 ,
, 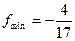 .
.
Домашнее задание.
Задание 3. Найти наибольшее и наименьшее значение функции  на указанном отрезке:
на указанном отрезке:
1) 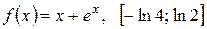
2) 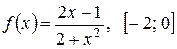
3) 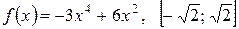
Ответы: 2.1) 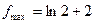 ,
, 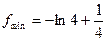 ; 2.2)
; 2.2) 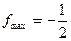 ,
, 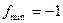 ;
;
2.3) 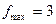 ,
, 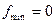 .
.
Производные высших порядков. Формула Тейлора.
 2015-05-10
2015-05-10 272
272








