Задание 1. Разложить функцию 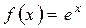 по степеням
по степеням 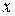 .
.
Решение:
Шаг 1. Найти производные функции  до
до 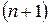 включительно:
включительно:
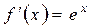
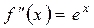
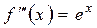
…
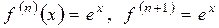
Шаг 2. Если все производные существуют в окрестности точки 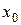 , то справедлива формула Тейлора (1). Для ее составления вычислить значения производных в точке
, то справедлива формула Тейлора (1). Для ее составления вычислить значения производных в точке 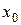 .
.
Поскольку в задаче требуется разложить функцию 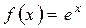 по степеням
по степеням 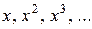 , то
, то 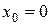 . Все производные существуют, вычислим их значения в точке
. Все производные существуют, вычислим их значения в точке 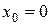 :
:
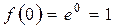
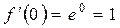
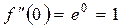
…
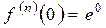
Шаг 3. Записать формулу Тейлора для функции 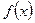 :
:
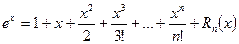 в окрестности точки
в окрестности точки 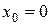 .
.
Задание 2. Вычислить приближенно 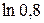 .
.
Решение:
Шаг 1. Определить значение какой функции  и в какой точке
и в какой точке 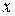 требуется вычислить.
требуется вычислить.
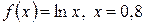 .
.
Шаг 2. Выбрать как можно ближе к точке 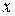 точку
точку 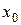 , в которой удобно вычислить значение функции
, в которой удобно вычислить значение функции 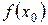 .
.
Выберем 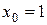 , т.к.
, т.к. 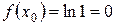 .
.
Шаг 3. Найти 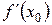
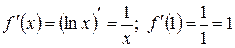
Шаг 4. Записать приближенное равенство (2) и произвести вычисления.
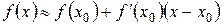
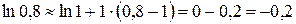 .
.
Т.о., 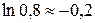 .
.
 2015-05-10
2015-05-10 266
266








