Параболы

Глава II. Элементы векторной алгебры и аналитической геометрии.

Тема 2. Кривые второго порядка. Полярная система координат.

ПАРАБОЛЫ.

ОПРЕДЕЛЕНИЕ 2.1 ПАРАБОЛА-ЭТО ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК РАВНОУДАЛЁННЫХ ОТ ЗАДАННОЙ ПРЯМОЙ И ФИКСИРОВАННОЙ ТОЧКИ НА ПЛОСКОСТИ (ТОЧКА НЕ ЛЕЖИТ НА ЗАДАННОЙ ПРЯМОЙ).ПРЯМАЯ НАЗЫВАЕТСЯ ДИРЕКТРИСОЙ, А ТОЧКА ФОКУСОМ ПАРАБОЛЫ (РИС.1). ПРЯМАЯ, ПРОХОДЯЩАЯ ЧЕРЕЗ ФОКУС И ПЕРПЕНДИКУЛЯРНАЯ ДИРЕКТРИСЕ НАЗЫВАЕТСЯ ОСЬЮ СИММЕТРИИ ПАРАБОЛЫ. ТОЧКА ПЕРЕСЕЧЕНИЯ ПАРАБОЛЫ С ОСЬЮ СИММЕТРИИ НАЗЫВАЕТСЯ ВЕРШИНОЙ ПАРАБОЛЫ.

М

ПРИМЕР 2.1 НАПИСАТЬ УРАВНЕНИЕ ПАРАБОЛЫ, КОТОРАЯ ИМЕЕТ ФОКУС (-1,0) И УРАВНЕНИЕ ДИРЕКТРИСЫ Х=1.РЕШЕНИЕ. ПУСТЬ ТОЧКА С КООРДИНАТАМИ М (х,у) ЛЕЖИТ НА ПАРАБОЛЕ. ТОГДА ПО ОПРЕДЕЛЕНИЮ 2.1 РАССТОЯНИЕ ОТ ТОЧКИ М ДО ФОКУСА РАВНО РАССТОЯНИЮ ОТ ТОЧКИ М ДО ДИРЕКТРИСЫ: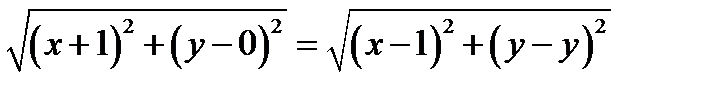

ВОЗВОДЯ ОБЕ ЧАСТИ В КВАДРАТ, ПОЛУЧАЕМ (рис.1)

.

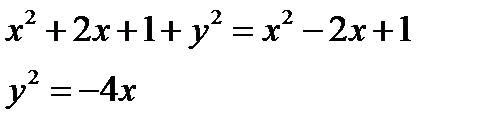рис.1 ИЛИ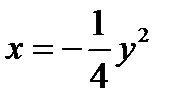

ПОЛУЧЕННОЕ УРАВНЕНИЕ ЯВЛЯЕТСЯ КАНОНИЧЕСКИМ УРАВНЕНИЕМ ПАРАБОЛЫ.

ТЕОРЕМА 2.1 ПАРАБОЛА НА ХУ ПЛОСКОСТИ ИМЕЮЩАЯ:

1)ВЕРШИНУ В НАЧАЛЕ КООРДИНАТ; 2)ФОКУС 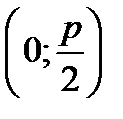НА ОСИ ОУ; 3) ДИРЕКТРИСУ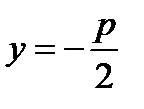

ИМЕЕТ УРАВНЕНИЕ 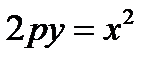(2.1)

У ПАРАБОЛЫ, ПРЕДСТАВЛЕННЙ НА РИС.2а, ПАРАМЕТР .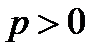

У ПАРАБОЛЫ, ПРЕДСТАВЛЕННОЙ НА РИС.2 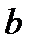,ПАРАМЕТР ..

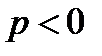РИС. 2а

ТЕОРЕМА 2.2 ПАРАБОЛА НА ОХУ ПЛОСКОСТИ ИМЕЮЩАЯ:

1)ВЕРШИНУ В НАЧАЛЕ КООРДИНАТ; 2)ФОКУС 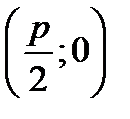НА ОСИ ОХ; 3) ДИРЕКТРИСУ 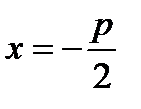ИМЕЕТ УРАВНЕНИЕ

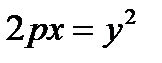(2.2)

У ПАРАБОЛЫ, ПРЕДСТАВЛЕННОЙ НА РИС.3а, ПАРАМЕТР .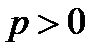

У ПАРАБОЛЫ, ПРЕДСТАВЛЕННОЙ НА РИС.3 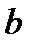, ПАРАМЕТР .

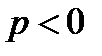РИС.3а